Grafisches Ableiten
-
Anstatt mit dem grafischen Ableiten kann man auch mit den Ableitungsregeln an das Thema
Ableitungsfunktion
anknüpfen.
Die beiden Kapitel zum grafischen Ableiten und zum rechnerischen Ableiten mit Ableitungsregeln sind unabhängig voneinander
konzipiert und können daher hinsichtlich der Reihenfolge ausgetauscht werden.
Worum geht es hier?
Mit der geometrischen Deutung der Ableitung als Steigung des Funktionsgraphen kann man sich schnell
einen ungefähren Überblick über alle Ableitungen einer Funktion verschaffen. Auf diese Weise erhält man
zeicherisch den Graph der Ableitungsfunktion.
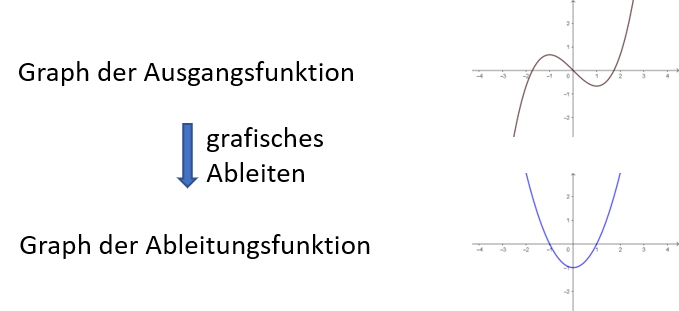
Für dieses Thema musst du ...
- ... sicher mit Funktionen umgehen können.
- ... das Konzept der Ableitung an einer Stelle verstanden haben.
- ... das Konzept der Ableitungsfunktion verstanden haben.
Hier lernst du, ...
- ... wie man den Graph einer Ableitungsfunktion durch grafisches Ableiten konstruiert.
- Das grafische Ableiten greift die geometrische Deutung der Ableitung auf und vernetzt sie mit der funktionalen Sicht auf die Ableitungsfunktion.
Das grafische Ableiten dient somit zur Vertiefung des Verständnisses zur Ableitungsfunktion.
- Für das grafische Ableiten stellen wir Applets zur Verfügung, mit denen die zentralen Schritte interaktiv durchgeführt werden können.
Parallel hierzu bieten wir Arbeitsblätter zum Download in, in denen das grafische Ableiten händisch durchgeführt werden muss.
Für den Unterricht empfehlen wir, beide Varianten zu nutzen.
- Das grafische Ableiten bereitet auch bereits auf Funktionsuntersuchungen vor. Bei der Konstruktion des Graphen der Ableitungsfunktiongelangt man
(fast) automatisch zu ersten Erkenntnissen über Zusammenhänge zwischen den Graphen der Ausgangsfunktion und der zugehörigen Ableitungsfunktion.
- Wir unterstützen dieses Herantasten an Zusammenhänge, indem wir es in in den Applets ermöglichen, selbst die zu bearbeiten Punkte einzustellen.
Hierdurch wird man angehalten, sich vorab Gedanken über
strukturell günstige Punkte
zu machen.


