Erkundung
Situation
Es geht wieder um das Laserschweißgerät. Hier muss der Laser verschiedene Nähte schweißen, die alle auf dem Grundvektor $\color{blue}\vec{a} = \begin{pmatrix}2\\1\end{pmatrix}$ beruhen: Mal ist die Naht länger als der Pfeil des Vektors $\vec{a}$, mal kürzer, mal fährt der Schweißkopf in entgegengesetzter Orientierung. Die Richtung soll aber immer dieselbe bleiben.
Aufgabe 1
Hier siehst du die Situation des Grundvektors. Der Programmierer hat $\color{blue}\vec{a} = \begin{pmatrix}2\\1\end{pmatrix}$ eingegeben und diese Naht erhalten: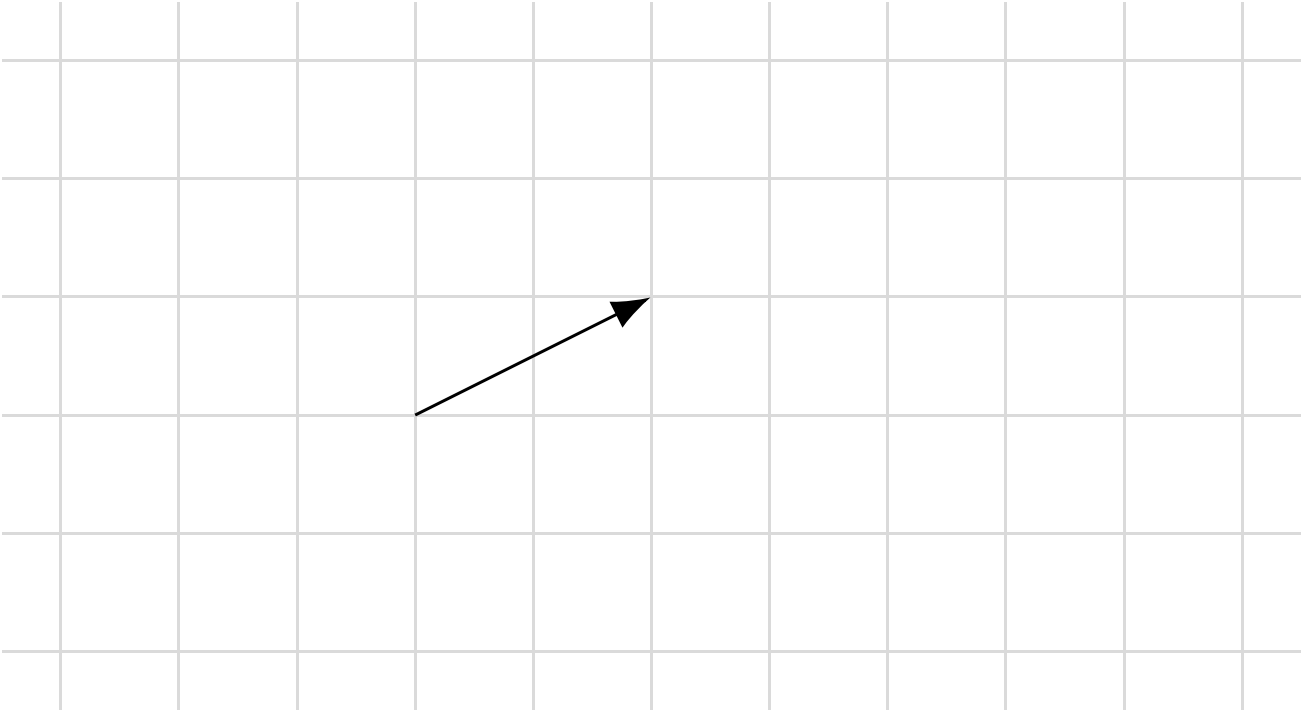
(a) Ermittle den Vektor $\vec{v_1}$, den man dem Laserschweißgerät eingeben müsste, um eine doppelt so lange Naht zu erhalten.
(b) Ermittle den Vektor $\vec{v_2}$, den man dem Laserschweißgerät eingeben müsste, um eine halb so lange Naht zu erhalten. (Gib Dezimalzahlen mit einem Punkt statt mit einem Komma ein.)
(c) Ermittle den Vektor $\vec{v_3}$, den man dem Laserschweißgerät eingeben müsste, um genauso lange Naht zu erhalten, die aber in die entgegengesetzte Richtung verläuft.
(d) Für Schnellere: Ermittle weitere Vektoren mit dem unten stehenden Applet.
Zum Herunterladen: skalarmultiplizieren4a.ggb
Aufgabe 3
Der Grundvektor $\vec{a} = \begin{pmatrix}6\\9\end{pmatrix}$ soll wieder verlängert bzw. verkürzt werden. Gib die Koordinaten der neuen Vektoren so an, dass ...
... $\vec{v_1}$ viermal so lang wie $\vec{v}$ ist.
... $\vec{v_2}$ zwei Drittel so lang wie $\vec{v}$ ist.
... $\vec{v_3}$ doppelt so lang wie $\vec{v}$ ist und in die entgegengesetzte Richtung zeigt.
... $\vec{v_4}$ halb so lang wie $\vec{v}$ ist und in die entgegengesetzte Richtung zeigt.

