Vertiefung

Die mittlere Änderungsrate bei einem Bewegungsvorgang deuten

Mit einem Fahrrad (heute E-Bike) kann man sehr gut die Welt erkunden. Jeder Kilometer kann mit interessanten Entdeckungen überraschen, aber auch ganz schön anstrengend sein.

Für die Auswertung von Touren gibt es heute Tracking-Apps, die dir verschiedenste Daten bereitstellen. Wir spielen eine solche Auswertung – in vereinfachter Form – hier durch.

Das Applet unter der Aufgabe zeigt ein Zeit-Weg-Diagramm zu einer Radtour. Auf der $x$-Achse ist die Zeit in h (Stunden) abgetragen, auf der $y$-Achse der zurückgelegte Weg in km (Kilometer). Der Graph der Funktion $f$ verdeutlicht den Ablauf der Radtour. Bearbeite die Aufgaben unter dem Applet. Nutze die Einblendungen im Applet zunächst noch nicht.

Zum Herunterladen: radtour.ggb

Aufgabe 1

(a) Kläre zunächst folgende Fragen:

• Wie lang hat die Radtour gedauert (in h)? Welche Strecke wurde dabei zurückgelegt (in km)?
• Wie erhält man hieraus die mittlere Geschwindigkeit (bzw. Durchschnittsgeschwindigkeit) der Radtour (in km/h)?
• Die Radtour führte über einen Berg. Wie kann man das am Graphen erkennen?
• Je steiler der Graph in einem Abschnitt, desto ... war die Geschwindigkeit in diesem Zeitraum.
• Wie würde der Graph aussehen, wenn man nach einer halben Stunde eine Reifenpanne hat und erst einmal für 15 Minuten nicht weiterfährt?

Blende die Animation ein und überprüfe, ob du die Geschwindigkeiten bei der Radtour richtig eingeschätzt hast.

(b) Blende das Werkzeug ein und bestimme die mittlere Geschwindigkeit der gesamten Radtour. Schätze auch die mittlere Geschwindigkeit ab, mit der der Berg beim Aufstieg bezwungen wurde und mit der die rasende Abfahrt stattfand.

Die mittlere Änderungsrate bei einem Temperaturverlauf deuten

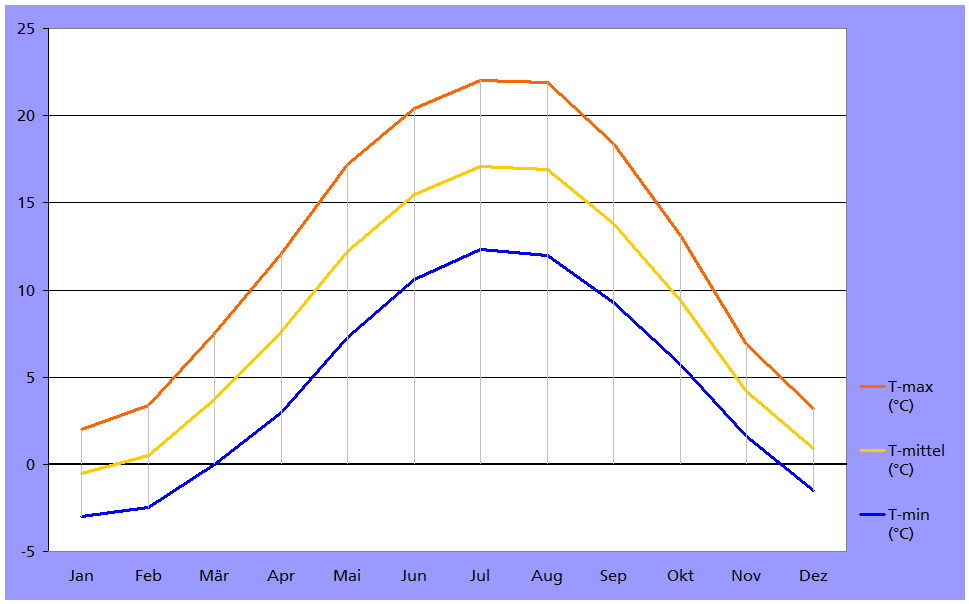
Die Temperatur ändert sich von Monat zu Monat. Die folgende Abbildung zeigt, wie sich die Temperatur in Deutschland während eines Jahres entwickelt. Betrachte nur den gelben Graph zur mittleren Tagestemperatur.

Aufgabe 2

(a) Der Graph steigt zuerst und fällt dann wieder. Was bedeutet das für die Temperaturentwicklung wärend eines Jahres.

(b) Schätze mit Hilfe des (gelben) Graphen ab, um wieviel °C pro Tag die Temperatur durchschnittlich in den Monaten Januar und April steigt. Erkläre, woran man am Graph direkt erkennt, dass der Wert im April größer als im Januar ist.

Mittlere Änderungsraten deuten

Was die mittlere Änderungsrate genau beschreibt hängt vom betrachteten Kontext ab. Fülle auch die linke Hälfte des Wissensspeichers zu Änderungsraten aus.