Übungen - Mittlere Änderungsrate

Aufgabe 1: Bevölkerungsentwicklung

Das Applet zeigt die bisherige Entwicklung der Weltbevölkerung mit einer Prognose bis zum Jahr 2100. Das Jahr 2000 entspricht dem $x$-Wert $0$. Die jeweiligen Bevölkerungszahlen sind in Milliarden angegeben. Bearbeite die Aufgaben unterhalb des Applets.

Zum Herunterladen: bevoelkerungsentwicklung2.ggb

(a) Wie groß war die Population in etwa im Jahr 1960? Wann erreicht die Population voraussichtlich die Grenze von 10 Milliarden Menschen?

(b) Bestimme die mittlere Änderungsrate zur Populationsentwicklung im Zeitintervall von $-20 \leq t \leq 20$. Bestimme auch die mittlere Änderungsrate zur Populationsentwicklung im Zeitintervall von $20 \leq t \leq 40$. Was fällt auf?

(c) Die mittlere Änderungsrate zur Populationsentwicklung in den Jahren zwischen 2000 und 2100 beträgt etwa 0.043 Milliarden pro Jahr. Bestätige zunächst diese Aussage mit einer Rechnung. Warum ist die folgende Aussage nicht korrekt: Die Population wächst in den Jahren zwischen 2000 und 2100 jedes Jahr um etwa 0.043 Milliarden Menschen. Wie könnte man es korrekt formulieren?

Aufgabe 2: Radtour

Mit einem Fahrrad (heute E-Bike) kann man sehr gut die Welt erkunden. Jeder Kilometer kann mit interessanten Entdeckungen überraschen, aber auch ganz schön anstrengend sein.

Für die Auswertung von Touren gibt es heute Tracking-Apps, die dir verschiedenste Daten bereitstellen. Wir spielen eine solche Auswertung – in vereinfachter Form – hier durch.

Das Applet unter der Aufgabe zeigt ein Zeit-Weg-Diagramm zu einer Radtour. Auf der $x$-Achse ist die Zeit in h (Stunden) abgetragen, auf der $y$-Achse der zurückgelegte Weg in km (Kilometer). Der Graph der Funktion $f$ verdeutlicht den Ablauf der Radtour.

Zum Herunterladen: radtour.ggb

Ziel ist es, die Radtour genauer zu beschreiben.

(a) Kläre zunächst folgende Fragen:

• Wie lang hat die Radtour gedauert (in h)?
• Welche Strecke wurde dabei zurückgelegt (in km)?
• Wie erhält man hieraus die mittlere Geschwindigkeit (bzw. Durchschnittsgeschwindigkeit) der Radtour (in km/h)?
• Die Radtour führte über einen Berg. Wie kann man das am Graphen erkennen?
• Je steiler der Graph in einem Abschnitt, desto ... war die Geschwindigkeit in diesem Zeitraum.
• Wie würde der Graph aussehen, wenn man nach einer halben Stunde eine Reifenpanne hat und erst einmal für 15 Minuten nicht weiterfährt?

(b) Mit den beiden Datenpunkten $P$ und $Q$ kannst du jetzt die Geschwindigkeiten bei der Tour genauer untersuchen. Bestimme die mittlere Geschwindigkeit im voreingestellten Zeitintervall.

(c) Schätze die mittlere Geschwindigkeit ab, mit der der Berg beim Aufstieg bezwungen wurde und mit der die rasende Abfahrt stattfand.

Aufgabe 3: Geschwindigkeiten bei einer Autofahrt

Das Applet unter der Aufgabe zeigt die Zeit-Weg-Funktion $s$, die für ein schnelles Auto die Entfernung vom Startpunkt (bzw die zurückgelegte Wegstrecke) (in m) in Abhängigkeit der Zeit (in s) beschreibt.

(a) Woran erkennt man direkt, dass das Auto immer schneller wird – also sich beschleunigt bewegt?

(b) Bestimme die mittlere Geschwindigkeit des Autos in den im Zeitintervall $0 \leq t \leq 2$, $2 \leq t \leq 4$, $4 \leq t \leq 6$, $6 \leq t \leq 8$ und $8 \leq t \leq 10$. Benutze die Funktionsgleichung $s(t) = 4t^2$. Kontrolliere die Ergebnisse im Applet.

(c) Rechne die in (b) ermittelten Geschwindigkeiten auch von $m/s$ in $km/h$ um. Es gilt $3.6 km/h = 1 m/s$. Sind die Ergebnisse realistisch?

Zum Herunterladen: porsche1.ggb

Aufgabe 4: Beschleunigung bei einer Autofahrt

Das Applet unter der Aufgabe zeigt die Entwicklung der Geschwindigkeit eines schnellen Autos mit der Zeit-Geschwindigkeit-Funktion $v$. Diese Funktion beschreibt die aktuelle Geschwindigkeit des Autos (in m/s) in Abhängigkeit der Zeit (in s).

(a) Woran erkennt man direkt, dass das Auto zwar immer schneller wird, aber nicht gleichmäßig beschleunigt? Wie schnell ist es nach 10s in km/h? Wann erreicht das Auto die Geschwindigkeit von 250 km/h? Benutze die Umrechnung $3.6 km/h = 1 m/s$.

(b) Bestimme die mittlere Änderungsrate zur Geschwindigkeitsentwicklung des Autos in den im Zeitintervall $0 \leq t \leq 2$, $2 \leq t \leq 4$, $4 \leq t \leq 6$, $6 \leq t \leq 8$ und $8 \leq t \leq 10$. Lies die benötigten Werte im Graph ab. Kontrolliere die Ergebnisse im Applet.

(c) Erläutere folgenden Zusammenhang: Die mittlere Änderungsrate bei einer Zeit-Geschwindigkeit-Funktion beschreibt die mittlere Beschleunigung im betreffenden Zeitintervall.

Zum Herunterladen: porsche2.ggb

Aufgabe 5: Diagrammanalyse

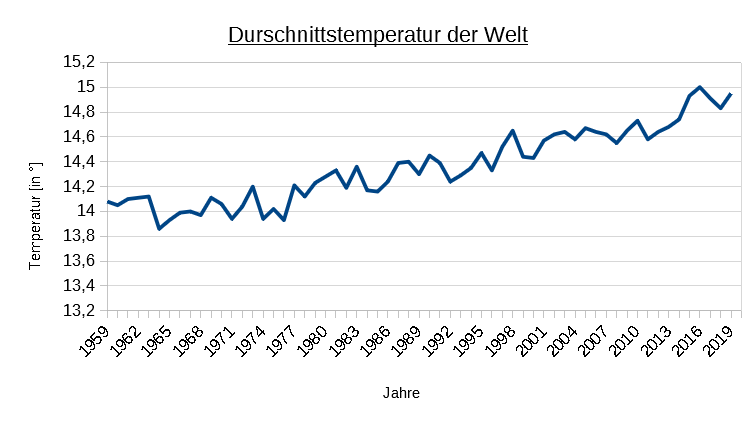
Das Diagramm verdeutlicht die Erderwärmung in den letzten Jahrzehnten.

(a) Bestimme die mittlere Änderungsrate zur Temperaturentwicklung im Zeitintervall $1959 \leq t \leq 2019$. Deute das Ergebnis.

(b) Die Temperaturentwicklung unterliegt vielen Schwankungen. Verdeutliche dies, indem du die mittlere Änderungsrate für passende Zeitintervalle bestimmst. Interessant sind Phasen mit einem deutlichen Anstieg und Phasen, in denen die Temperatur wieder zurückgegangen ist.

Aufgabe 6: Diagrammanalyse

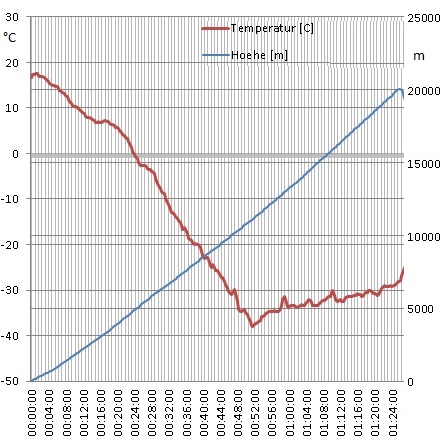
Das Diagramm zeigt Messungen von einer Ballon-Fahrt vom 27. September 2013 ab 12:40 in Stölln/Rhinow.

(a) Betrachte die Zuordnung „Zeit [min] -> Temperatur [°C]“. Bestimme die mittlere Änderungsrate für diese Zuordnung im Zeitintervall $0 \leq t \leq 52$. Warum muss ein negativer Wert herauskommen? Begründe kurz.

(b) Aus dem Diagramm kann man auch die Zuordnung „Höhe [m] -> Temperatur [°C]“ rekonstruieren. Bestimme die mittlere Änderungsrate für diese Zuordnung im Höhenintervall $0 \leq h \leq 10000$.

(c) Erläutere mit den beiden Aufgabenteilen: Eine Änderungsrate bezieht sich nicht immer auf eine zeitliche Entwicklung. Eine Änderungsrate bzw. Änderungsgeschwindigkeit kann auch auf eine anderen Größe bezogen werden.

Aufgabe 7: Änderungsraten bei beliebigen Funktionen

Bestimme die mittlere Änderungsrate der Funktion $f$ im jeweils angegebenen Intervall. Kontrolliere die Ergebnisse mit dem Applet.

• geg.: $f(x) = x^2$
  ges.: $m(2, 5)$ und $m(-2, 2)$
• geg.: $f(x) = 2x$
  ges.: $m(1, 4)$ und $m(4, 7)$
• geg.: $f(x) = \displaystyle \frac{1}{x}$
  ges.: $m(1, 4)$ und $m(1, 2)$
• geg.: $f(x) = 3$
  ges.: $m(1, 7)$ und $m(3, 5)$
• geg.: $f(x) = x^2$
  ges.: $x_1$ mit $m(0, x_1) = 4$

Applet zur Kontrolle

Zum Herunterladen: plotter_aenderungsrate.ggb

Aufgabe 8: Formeln für Änderungsraten bei beliebigen Funktionen

Leite die folgenden Formeln für mittlere Änderungsraten her.

(a) Für eine konstante Funktion $f$ mit $f(x) = a$ gilt: $m(x_0,x_1) = 0$.

(b) Für eine lineare Funktion $f$ mit $f(x) = ax + b$ gilt: $m(x_0,x_1) = a$.

(c) Für eine quadratische Funktion $f$ mit $f(x) = ax^2$ gilt: $m(x_0,x_1) = a(x_0+x_1)$.