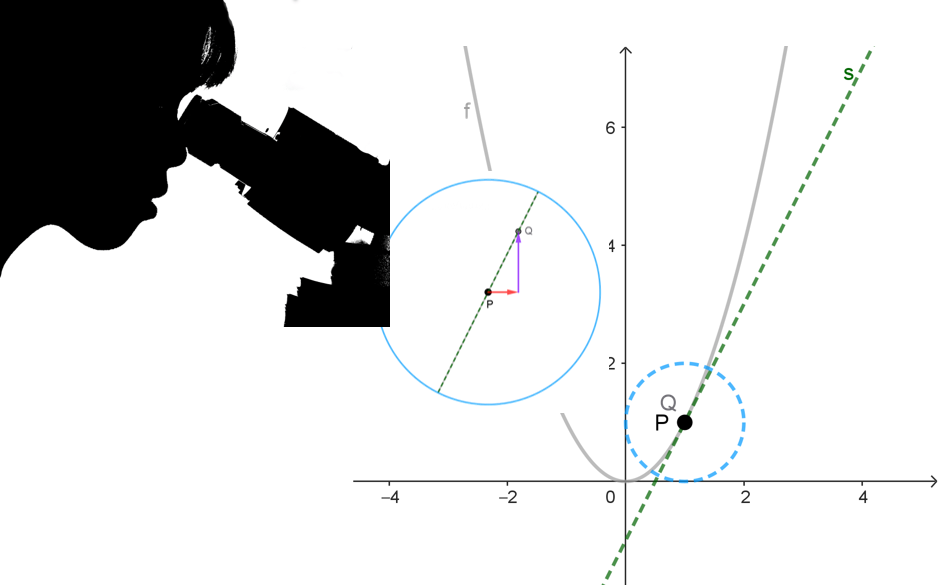
Ableitung als lokale Änderungsrate

Worum geht es hier?

Im letzten Kapitel wurden Änderungsraten bestimmt, die sich immer auf ein $x$-Werte-Intervall bezogen haben. In diesem Kapitel werden wir das Intervall immer kleiner machen und damit zur lokalen Änderungsrate übergehen. Die dabei gewonnenen Erkenntnisse werden anschließend verallgemeinernd mit dem Ableitungsbegriff beschrieben.

Für dieses Thema musst du ...

• ... sicher mit Funktionen umgehen können.
• ... das Konzept der mittleren Änderungsrate verstanden haben.

Hier lernst du, ...

• ... was man unter einer lokalen Änderungsrate versteht.
• ... wie man eine lokale Änderungsrate bestimmt.
• ... was man unter einer Ableitung versteht.
• ... wie man eine Ableitung an einer Stelle näherungsweise bestimmt.
• ... wie man eine Ableitung an einer Stelle geometrisch deutet.
• ... wie man eine Ableitung an einer Stelle berechnet.