Zusammenfassung - Problemlösen mit linearen Gleichungssystemen
Rückblick
Die Anwendungsbeispiele in den letzten Abschnitten zeigen, dass das Lösen von linearen Gleichungssystemen oft ein zentraler Schritt beim Lösen eines Problems ist. Die folgende Übersicht verdeutlicht die Vorgehensweise.
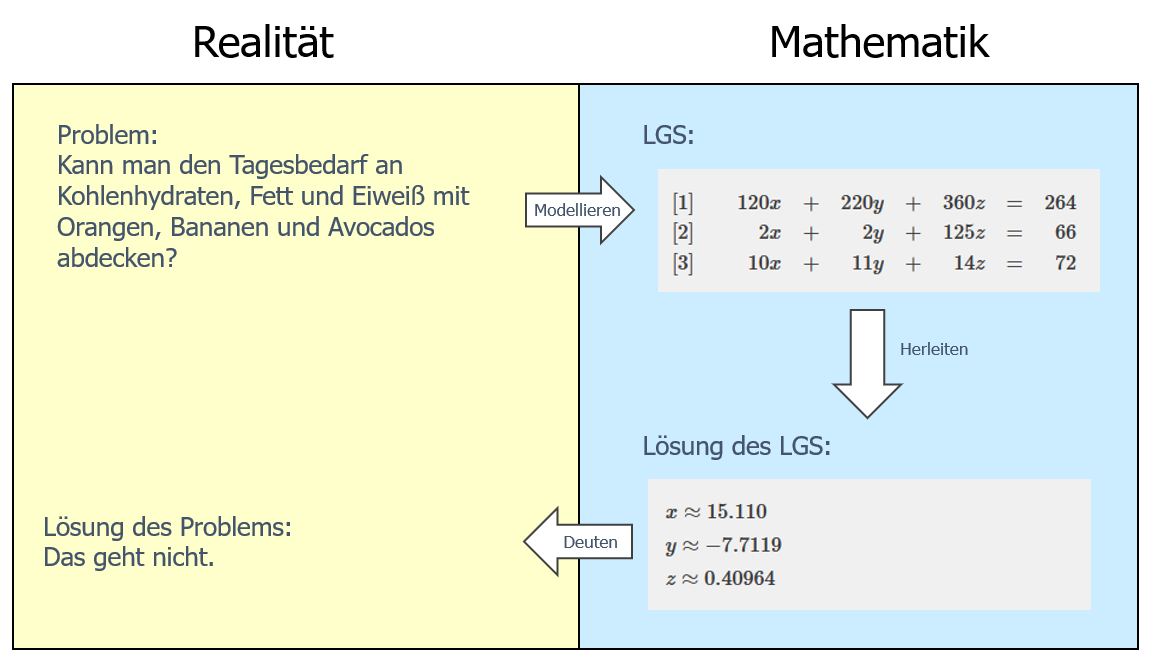
Beim Modellieren wird die Problemsituation mit Hilfe von (oft mehreren) Gleichungen beschrieben. Das Lösen der Gleichungen erfolgt dann mit geeigneten innermathematischen Verfahren. Die Lösungen der Gleichungen müssen abschließend im Problemkontext gedeutet und bewertet werden.
Lineare Gleichungssysteme
In der Übersicht oben kommt das folgende lineare Gleichungssystem vor:
$\begin{array}{lrcrcrcr} [1] &\quad 120x & + & 220y & + & 360z & = & 264 \\ [2] &\quad 2x & + & 2y & + & 125z & = & 66 \\ [3] &\quad 10x & + & 11y & + & 14z & = & 72 \end{array}$
Es besteht aus $3$ Gleichungen mit den $3$ Variablen $x$, $y$ und $z$. Die Gleichungen sind lineare Gleichungen, da die Variablen ausschließlich mit Zahlen multipliziert werden (und nicht potenziert oder mit anderen Variablen multipliziert werden).
Ein lineares Gleichungssystem (kurz: LGS) besteht aus (meist) mehreren linearen Gleichungen mit fest vorgegebenen Variablen.
In der folgenden Tabelle sind einige Beispiele aufgeführt.
| Beschreibung | Gleichungssystem |
|---|---|
| LGS mit $2$ Gleichungen und $2$ Variablen | $\begin{array}{lrcrcrcr} [1] &\quad x &+& 3y & = & 15.15 \\ [2] &\quad 2x &+& y & = & 14.05 \end{array}$ |
| LGS mit $5$ Gleichungen und $5$ Variablen | $\begin{array}{lrcrcrcr} [1] &\quad x_1 + x_2 & = & 12 \\ [2] &\quad x_2 + x_3 & = & 13.5 \\ [3] &\quad x_3 + x_4 & = & 11.5 \\ [4] &\quad x_4 + x_5 & = & 8 \\ [5] &\quad x_1 + x_3 + x_5 & = & 11 \end{array}$ |
| LGS mit $3$ Gleichungen und $2$ Variablen | $\begin{array}{lrcrcrcr} [1] &\quad x &+& 3y & = & 15.15 \\ [2] &\quad 2x &+& y & = & 14.05 \\ [3] &\quad x &+& y & = & 8.65 \\ \end{array}$ |
| LGS mit $4$ Gleichungen und $5$ Variablen | $\begin{array}{lrcrcrcr} [1] &\quad x_1 + x_2 + x_3 & = & 24 \\ [2] &\quad x_2 + x_3 + x_4 & = & 21 \\ [3] &\quad x_3 + x_4 + x_5 & = & 28 \\ [4] &\quad x_1 + x_3 + x_3 + x_4 + x_5 & = & 46 \end{array}$ |
| LGS mit $2$ Gleichungen und den $2$ Variablen $x$ und $y$ | $\begin{array}{lrcrcrcr} [1] &\quad a\cdot x &+& b \cdot y & = & u \\ [2] &\quad c\cdot x &+& d \cdot y & = & v \end{array}$ |
| LGS mit $3$ Gleichungen und den $3$ Variablen $x_1$, $x_2$ und $x_3$ | $\begin{array}{lrcrcrcr} [1] &\quad a_{11} \cdot x_1 &+& a_{12} \cdot x_2 & + & a_{13} \cdot x_3 & = & b_{1} \\ [2] &\quad a_{21} \cdot x_1 &+& a_{22} \cdot x_2 & + & a_{23} \cdot x_3 & = & b_{2} \\ [3] &\quad a_{31} \cdot x_1 &+& a_{32} \cdot x_2 & + & a_{33} \cdot x_3 & = & b_{3} \\ \end{array}$ |
Man sieht, dass die Variablen unterschiedlich benannt werden können. Üblich sind die Bezeichner $x$, $y$ und $z$ sowie $x_1$, $x_2$, ... .
Man sieht auch, dass die Anzahl der Gleichungen nicht mit der Anzahl der Variablen übereinstimmen muss.
In den beiden letzten verallgemeinerten Beispielen ist es wichtig zu klären, welche Bezeichner für Variablen und welche für verallgemeinerte Koeffizienten stehen.
Ausblick
Ziel der folgenden Kapitel ist es, das Lösen linearer Gleichungssysteme genauer zu untersuchen. Dabei sollen u.a. folgende Fragen geklärt werden:
- Wie viele Lösungen kann ein lineares Gleichungssystem haben?
- Wie kann man systematisch beim Lösen von linearen Gleichungssystemen vorgehen?
- Gib es strukturelle Zusammenhänge über Lösungen linearer Gleichungssysteme?

