Erarbeitung - Lösung des Problems

Das Problem präzisieren

Gegeben sind die Werte für die durchschnittliche Anzahl der Schwerverkehrsteilnehmer, die pro Stunde auf das Autobahnkreuz zu bzw. vom Autobahnkreuz wegfahren.

[1]

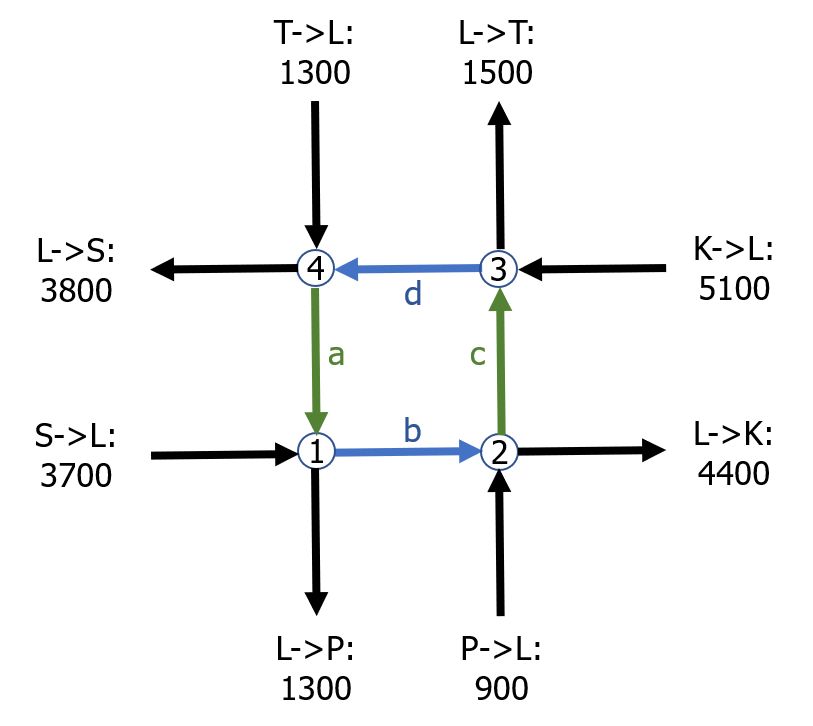
Gesucht sind die Werte für die durchschnittliche Anzahl der Schwerverkehrsteilnehmer, die pro Stunde die Autobahnbrücke über- bzw. unterqueren. Diese Werte werden mit $a$, $b$, $c$, $d$ bezeichnet.

Die Verkehrsdichten am Autobahnkreuz Landstuhl-West werden von den Zählstellen nur näherungsweise erfasst. Es kommt öfters mal vor, dass ein LKW von einer Zählstelle nicht registriert wird. Wir benutzen daher im Folgenden gerundete Werte, die sich an den gemessenen Werten orientieren.

[2]

Aufgabe 1

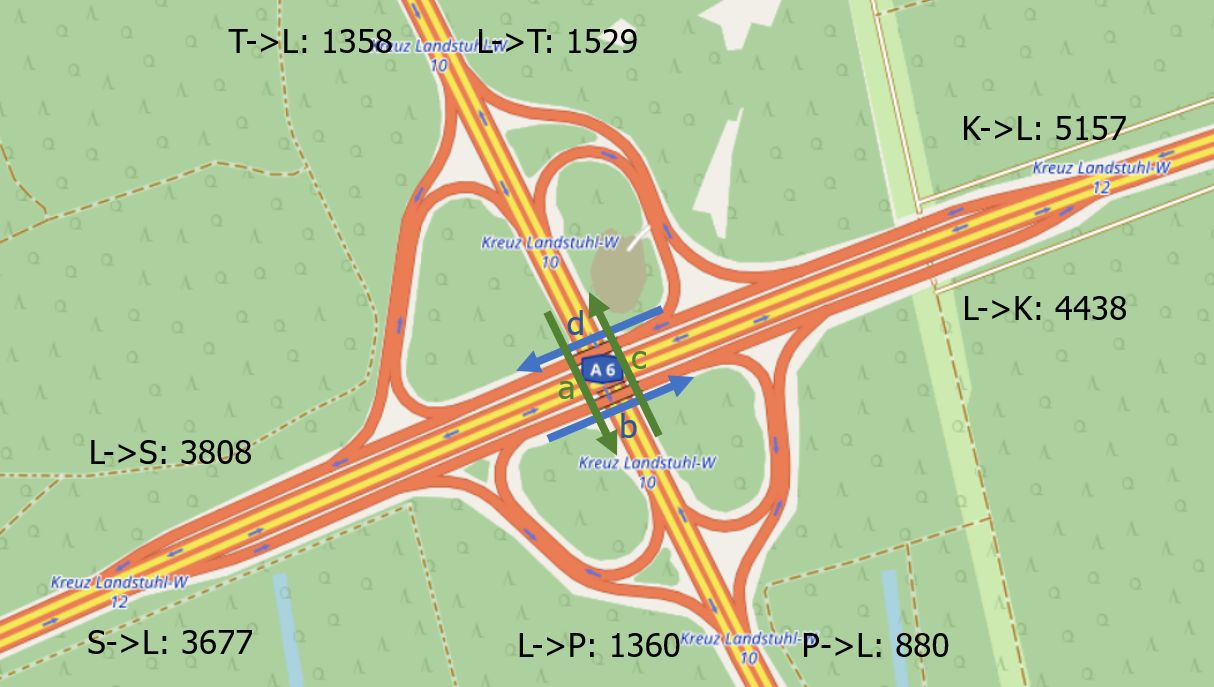
Erläutere die Darstellung. Erkläre wie ein LKW im realen Autobahnkreuz bzw. im vereinfachten Modell von Saarbrücken nach Trier fährt.

Das Problem mit einem LGS lösen

Zwischen den verschiedenen Verkehrsangaben gibt es Zusammenhänge. Diese lassen sich mit einem linearen Gleichungssystem beschreiben.

$\begin{array}{lrcrcrcr} [1] &\quad 3700 + a & = & 1300 + b \\ [2] &\quad ... \\ [3] &\quad ... \\ [4] &\quad ... \end{array}$

Aufgabe 2

(a) Deute die Gleichung $[1]$ als Ein- und Ausfuhrbilanz: Alle LKWs, die von $S$ oder vom Abschnitt $a$ aus kommen, ...

(b) Stelle entsprechende Gleichungen für die anderen Knotenpunkte auf.

Aufgabe 3

Wenn man bei diesem LGS die Stategie "Gleichungen nach bestimmten Variablen auflösen und die Ergebnisse in andere Gleichungen einsetzen" benutzt, erhält man eine Gleichung, die immer erfüllt ist (z.B. $a = a$). Probiere das selbst aus.

Aufgabe 4

Das LGS hat unendlich viele Lösungen. Wir geben für $c$ eine beliebige reelle Zahl $t$ vor und bestimmen dann die Werte der anderen Variablen.

(a) Probiere das für $c = 100$ aus. Bestimme mit dieser Vorgabe die Werte für $a$, $b$ und $d$.

(b) Zeige ganz allgemein. Wenn man $c = t$ mit einer reellen Zahl $t$ vorgibt, dann erhält man folgende Lösung des LGS:.

• $a = t + 1100$
• $b = t + 3500$
• $c = t$
• $d = t + 3600$

Aufgabe 5

(a) Kann man tatsächlich jede reelle Zahl als sinnvolle Lösung im Kontext ansehen? Beurteile die Wahl $t = -100$. Begründe, dass $t$ folgende Bedingung erfüllen muss:

$t \geq 0$

(b) Wie viele LKW fahren maximal pro Stunde in das Autobahnkreiz rein? Warum ist $t = 1000000$ nicht möglich? Begründe, dass die folgende Bedingung immer erfüllt sein muss:

$a + b + c + d \leq 11000$

Was würde es in der Realität bedeuten, wenn $a + b + c + d = 11000$ gelten würde? Erkläre kurz.

(c) Setze die oben aufgeführten Ergebnisse für $a$, $b$, $c$, $d$ in die Ungleichung $a + b + c + d \leq 11000$ ein und folgere hieraus, dass diese Bedingung für $t$ gelten muss:

$t \leq 700$

(d) Mit welchem maximalen LKW-Verkehrsaufkommen muss man am Autobahnkreuz Landstuhl-West in den Abschnitten $a$, $b$, $c$ und $d$ rechnen, wenn man die oben angegebenen (gerundeten) Messwerte zu Grunde legt? Bestimme abschließend diese Werte.