Einstieg - Zielsetzung
Zur Orientierung
In den Erkundungen zum Begrüßungsproblem und zu den Türmen von Hanoi wurden Zahlenfolge benutzt, um die jeweiligen Probleme zu bearbeiten. Wir lösen uns jetzt von den speziellen Zahlenfolgen und betrachten das verallgemeinerte Zahlenfolgenkonzept.
Problemlösen mit Zahlenfolgen
| Beispiel 1: Begrüßungen | Beispiel 2: Türme von Hanoi |
|---|---|
|
In einem Raum befinden sich zahlreiche Personen. Jede Person soll jede andere begrüßen.
Wie viele Begrüßungen finden dann statt?
|
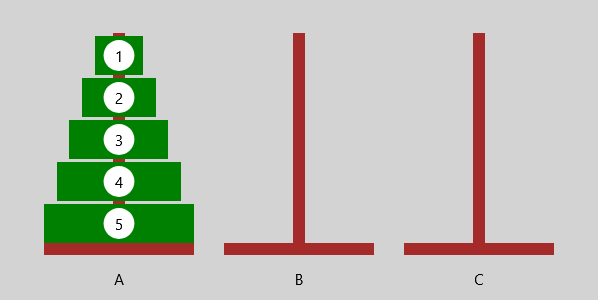
Die Scheiben des Ausgangsstapels sollen nach vorgegebenen Regeln auf einen Endstapel umgeschichtet werden.
Wie viele Scheibenbewegungen sind hierzu erforderlich?
|
| Die Zahlenfolge $0; 1; 3; 6; 10, ...$ beschreibt die Anzahl der Begrüßungen bei $1; 2; 3; 4; 5; ...$ Personen. | Die Zahlenfolge $1; 3; 7; 15; 31, ...$ beschreibt die Anzahl der Bewegungen bei einem Ausgangsstapel mit $1; 2; 3; 4; 5; ...$ Scheiben. |
Zielsetzung
Die Beispiele zeigen, dass Zahlenfolgen ein nützliches Werkzeug der Mathematik sind.
Ziel der folgenden Kapitel ist es, das Zahlenfolgenkonzept genauer zu untersuchen.
In einem ersten Schritt werden wir hier den Begriff Zahlenfolge
präzisieren.

