Exkurs - Lösungsverfahren
Zur Orientierung
Wir haben bereits eine Strategie entwickelt, wie man Türme beliebiger Höhe umschichtet. Auf dieser Seite geht es darum, diese Strategie als ein Lösungsverfahren (man nennt das einen Algorithmus) zu formulieren. Außerdem wird die dahinter liegende Idee vertieft. Für die weitere Bearbeitung des Kapitels ist dieser Abschnitt nicht erforderlich.
Zielsetzung
Auf eine Lösung zurückgreifen
Wir betrachten das Umschichtungsproblem für $n = 5$ Scheiben.
Problem: Transportiere einen 5-Scheiben-Turm von A über B nach C.
Ein Löseverfahren könnte so aussehen:
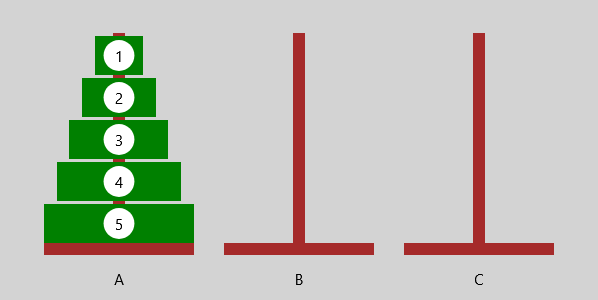
|

|
| Bewege einen 5-Scheiben-Turm zum Endstapel | Bewege einen 4-Scheiben-Turm zum Hilfsstapel |
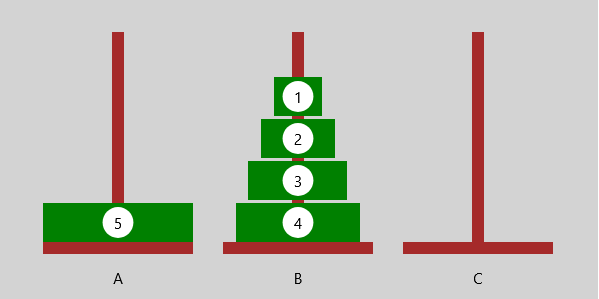
|
|
| Bewege 1 Scheibe zum Endstapel | |
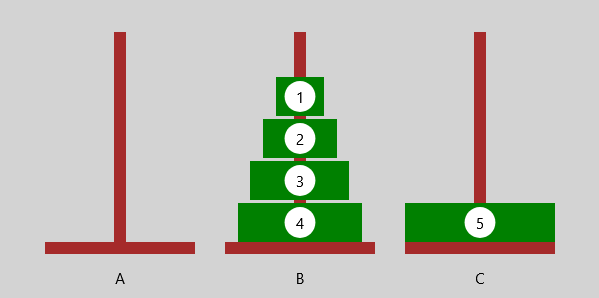
|
|
| Bewege einen 4-Scheiben-Turm zum Endstapel | |
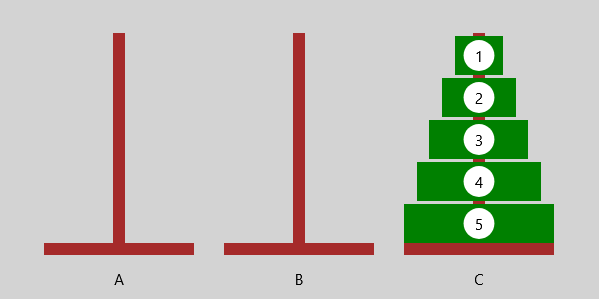
|

|
Aufgabe 1
Die Lösung zum Ausgangsproblem weist eine Besonderheit auf. Sie beschreibt nicht jeden einzelnen Scheibentransport. Die Lösung besteht vielmehr darin, das Ausgangsproblem auf ein entsprechendes Problem in verkleinerter Form zu reduzieren. Man nennt diese Strategie rekursive Problemreduktion.
Erläutere diese Problemlösestrategie am Beispiel "Bewege einen 5-Scheiben-Turm von A über B nach C".
Ein Löseverfahren für die Türme von Hanoi allgemein formulieren
Wir beschreiben das Problem zunächst verallgemeinernd.
Problem: Bewege einen n-Scheiben-Turm
von einem Ausgangsstapel X
über einen Hilfsstapel Y
zu einem Zielstapel Z.
Die oben beschriebene Lösungsidee wird jetzt zu einem Lösungsalgorithmus verallgemeinert.
ALGORITHMUS bewege einen n-Scheiben-Turm von X über Y nach Z:
wenn n > 1:
bewege einen (n-1)-Scheiben-Turm von X über Z nach Y
bewege eine Scheibe von X nach Z
bewege einen (n-1)-Scheiben-Turm von Y über X nach Z
sonst:
bewege eine Scheibe von X nach Z
Hier sind n, X, Y und Z
Parameter, die bei konkreten Problemstellungen aktualisiert werden müssen.
Aufgabe 2
Dass der Algorithmus tatsächlich das allgemeine Umschichtungsproblem löst, zeigt sich, wenn man sämtliche Schritte ausführt.
Verdeutliche das am Beispiel eines 3-Scheiben-Turms. Erkläre hierzu die folgendenden Ausführungen.
Ausführungstiefe 1:
bewege einen 3-Scheiben-Turm von A über B nach C:
bewege einen 2-Scheiben-Turm von A über C nach B
bewege eine Scheibe von A nach C
bewege einen 2-Scheiben-Turm von B über A nach C
Ausführungstiefe 2:
bewege einen 3-Scheiben-Turm von A über B nach C:
bewege einen 2-Scheiben-Turm von A über C nach B:
bewege einen 1-Scheiben-Turm von A über B nach C
bewege eine Scheibe von A nach B
bewege einen 1-Scheiben-Turm von C über A nach B
bewege eine Scheibe von A nach C
bewege einen 2-Scheiben-Turm von B über A nach C:
bewege einen 1-Scheiben-Turm von B über C nach A
bewege eine Scheibe von B nach C
bewege einen 1-Scheiben-Turm von A über B nach C
Ausführungstiefe 3:
bewege einen 3-Scheiben-Turm von A über B nach C:
bewege einen 2-Scheiben-Turm von A über C nach B:
bewege einen 1-Scheiben-Turm von A über B nach C:
bewege eine Scheibe von A nach C
bewege eine Scheibe von A nach B
bewege einen 1-Scheiben-Turm von C über A nach B:
bewege eine Scheibe von C nach B
bewege eine Scheibe von A nach C
bewege einen 2-Scheiben-Turm von B über A nach C:
bewege einen 1-Scheiben-Turm von B über C nach A:
bewege eine Scheibe von B nach A
bewege eine Scheibe von B nach C
bewege einen 1-Scheiben-Turm von A über B nach C:
bewege eine Scheibe von A nach C
Wenn man jetzt alle Aufrufe des Algorithmus weglässt, dann ergibt sich eine Folge von Basisaktionen, die letztlich das Problem löst.
bewege eine Scheibe von A nach C
bewege eine Scheibe von A nach B
bewege eine Scheibe von C nach B
bewege eine Scheibe von A nach C
bewege eine Scheibe von B nach A
bewege eine Scheibe von B nach C
bewege eine Scheibe von A nach C

