Knobelprobleme

Aufgabe 1 - eine Streichholzfigur legen

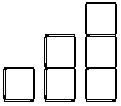
Mit Streichhölzern kann man Figuren legen. Die Abbildung zeigt eine Möglichkeit, wie man Streichholztürme erstellen kann.

Für den 1. Turm benötigt man 4 Streichhölzer, für den 2. Turm 7 Streichhölzer. Das sieht man direkt. Wie viele Streichhölzer benötigt man für den 10. bzw. 100. Turm?

Löse das Problem mit einer Zahlenfolge.

Aufgabe 2 - ein Kartenhaus bauen

Mit Spielkarten kann man Kartenhäuser bauen. Die Abbildung zeigt eine Möglichkeit, wie man das machen kann.

Für das 1. Kartenhaus benötigt man 3 Karten, für den 2. Kartenhaus 9 Karten. Das erhält man direkt durch Abzählen. Wie viele Karten benötigt man für das 10. bzw. 100. Kartenhaus?

Löse das Problem mit einer Zahlenfolge.

Aufgabe 3 - Punktmuster beschreiben

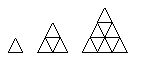
Betrachte die unten dargestellten Punktmuster. Wähle deine Punktmuster aus und beschreibe die zugehörigen Folgen mit einer expliziten und/oder rekursiven Darstellung. Beachte: Der Schwierigkeitsgrad erhöht sich nach unten hin.

Punktmuster A:

$a_n$: Anzahl der Punkte der $n$-ten Figur (für $n = 1; 2; 3; ...$)

Punktmuster B:

$a_n$: Anzahl der Punkte der $n$-ten Figur (für $n = 1; 2; 3; ...$)

Punktmuster C:

$a_n$: Anzahl der Punkte der $n$-ten Figur (für $n = 1; 2; 3; ...$)

Punktmuster D:

$a_n$: Anzahl der Punkte der $n$-ten Figur (für $n = 1; 2; 3; ...$)

Punktmuster E:

$a_n$: Anzahl der roten Punkte im Innenraum der $n$-ten Figur (für $n = 1; 2; 3; ...$)

Punktmuster F:

$a_n$: Anzahl der Kugeln zur $n$-ten Figur (für $n = 1; 2; 3; ...$)

Beachte: Die Abbildung zeigt nur die 4. Figur (mit 4 Kugeln entlang der Grundseite der Pyramide).