Nullstellen - abc-Lösungsformel
Zur Orientierung
Eine Nullstelle einer Funktion $f$ ist eine Zahl (bzw. Stelle) $\textcolor{red}{x}$, die die Bedingung $f(\textcolor{red}{x}) = 0$ erfüllt.
Anschaulich ist eine Nullstelle eine Stelle, an der der Graph der Funktion die $x$-Achse schneidet oder berührt.
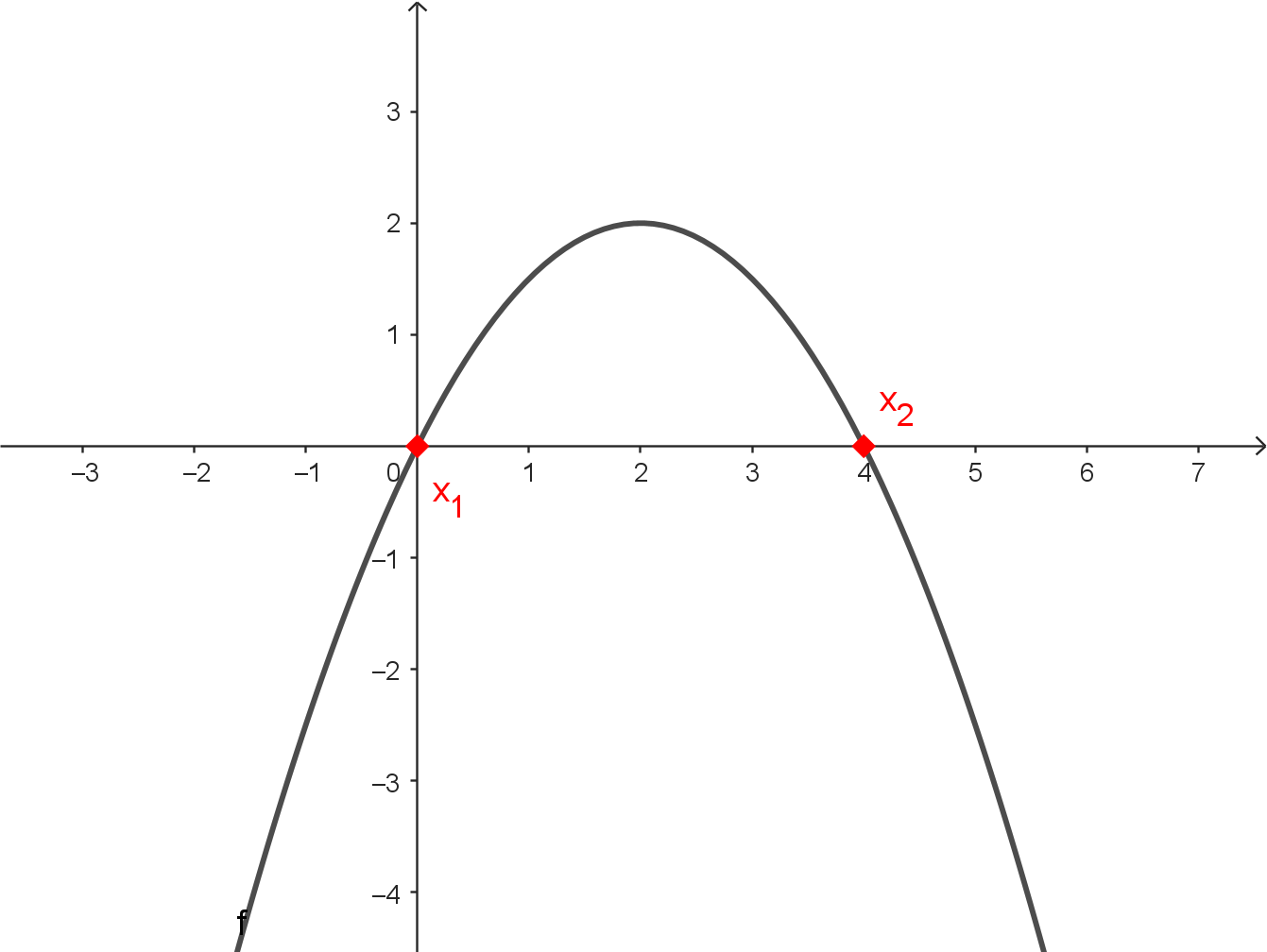
Im letzten Abschnitt wurden die Nullstellen einer quadratischen Funktion mit Hilfe von Basisstrategien bestimmt. Diese Strategien sind allerdings nur in speziellen Parameter-Situationen anwendbar. Wir betrachten hier eine Strategie, die immer anwendbar ist. Wir benutzen hierzu eine Lösungsformel zur Bestimmung der Nullstellen einer quadratischen Funktion. Beachte, dass diese Formel komplex (und daher bei der Verwendung auch fehleranfällig) ist. Versuche daher immer erst, eine Basisstrategie bei der Nullstellenbestimmung anzuwenden.
Eine Lösungsformel verwenden
Im folgenden Applet wird die sogenannte abc-Formel zur Nullstellenbestimmung bei quadratischen Funktionen benutzt.
Zum Herunterladen: nullstellenqf.ggb
Aufgabe 1
Mache dich nochmal mit der abc-Formel vertraut. Erkläre anhand des Applets, wie man mit dieser Formel die Nullstellen einer quadratischen Funktion bestimmt.
Aufgabe2
Bestimme analog die Nullstellen der folgenden Funktionen.
- $f(x) = x^2 - 5x + 4$
- $f(x) = x^2 + x -2$
- $f(x) = x^2 - 4x +4$
- $f(x) = \frac{1}{10}x^2 - \frac{3}{2}x +5$
- $f(x) = x^2 + 2$

