Beschreibung von Bewegungen

Tennisspiele beschreiben

Unser Ziel hier ist es, Tennisspiele (in vereinfachter Form) mathematisch zu beschreiben.

Zwei Tennisspieler(innen) – A und B – tragen ein Spiel aus. Das Spielfeld sei (etwas vereinfacht) 2-mal 12 Meter lang. Wir betrachten nur den jeweiligen Abstand des Tennisballs von der Grundlinie im Feld von A.

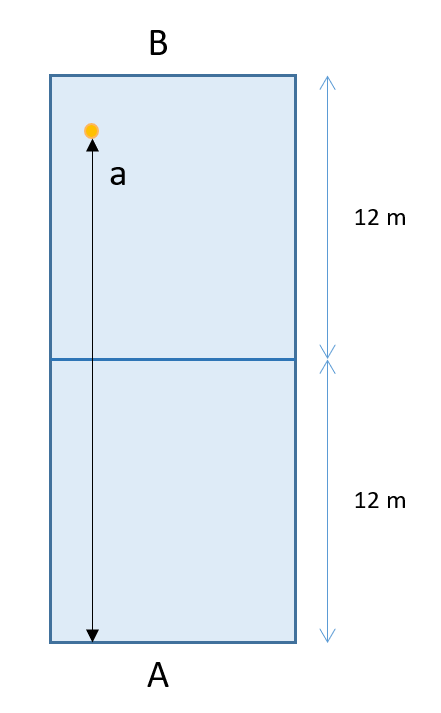
Einen Ballwechsel beschreiben wir mit der folgenden Zuordnung:

Zeit [in s] $\rightarrow$ Abstand des Balls von der Grundlinie bei A [in m].

Im Applet wird ein Ballwechsel stark vereinfacht in einem Zeit-Weg-Diagramm dargestellt. Auf der $x$-Achse wird hier die Zeit in Sekunden dargestellt, auf der $y$-Achse die Entfernung von der Grundlinie bei A in Meter. Der Graph beschreibt die Bewegung des Balls. Im linken Fenster kann man den Ballwechsel simulieren. Benutze die Simulation aber nur zur Kontrolle. Bearbeite immer zuerst die Aufgaben.

Zum Herunterladen: tennis.ggb

Aufgabe 1

Kläre folgende Fragen:

• Was beschreiben die Punkte auf dem Graph? Was kann man aus den Koordinaten der Punkte herauslesen?
• Woran erkennt man, dass A aufschlägt?
• Wie lang dauert der Flug des Balls, bis er „returniert“ wird? Wo etwa erfolgt der Return?
• Woran erkennt man, dass der Ball nach dem zweiten Schlag von A langsamer ist als nach dem Aufschlag?
• Was könnte zum Zeitpunkt $t = 2.75$ geschehen sein? Kann man entscheiden, wer den Ballwechsel gewonnen hat?

Aufgabe 2

Der zweite Ballwechsel verläuft wie folgt: B schlägt auf. Es ist bekannt, dass B einen härteren Aufschlag als A hat. A returniert. B schlägt den Ball nahe am Netz volley zurück, leider aber ins Aus hinter die Grundlinie.

Bewege die Punkte im Koordinatensystem so, dass der Graph den Spielverlauf in etwa wiedergibt.

Aufgabe 3

Im Koordinatensystem ist die Zeit auf der $x$-Achse und der Abstand des Balls von der Grundlinie bei A auf der $y$-Achse aufgetragen. Warum hat man sich für diese Achsenwahl entschieden? Erläutere kurz.