Überprüfung - Diagnosetest

Aufgabe 1: Funktion als Zuordnung

(a) Betrachte die Temperaturentwicklung an einem normalen Tag. Welche der folgenden Zuordnungen stellt eine Funktion dar?

• Uhrzeit $\rightarrow$ Temperatur
• Temperatur $\rightarrow$ Uhrzeit

(b) Wo trägt man sinnvollerweise Temperatur und Uhrzeit in einer Wertetabelle ein? Ersetze die Punkte durch konkrete Angaben.

Größe 1: ...	Größe 2: ...
...	...
...	...
...	...

(c) Welche Größe wird sinnvollerweise auf welcher Achse im Koordinatensystem abgetragen?

• $x$-Achse: ...
• $y$-Achse: ...

Skizziere einen Temperaturverlauf. Benutze hierzu den Stift (im Auswahlmenu zum Zeiger).

Zum Herunterladen: temperaturentwicklung.ggb

Kontrolle

(a)

• Uhrzeit $\rightarrow$ Temperatur: Die Zuordnung ist eindeutig. Die Zuordnung stellt also eine Funktion dar.
• Temperatur $\rightarrow$ Uhrzeit: Die Zuordnung ist (an einem normalen Tag) nicht eindeutig. Die Zuordnung stellt also keine Funktion dar.

(b)

Größe 1: Uhrzeit [in h]	Größe 2: Temperatur [in °C]
6	10
12	25
22	10

(c)

• $x$-Achse: Uhrzeit
• $y$-Achse: Temperatur

Aufgabe 2: Darstellung einer Funktion

Betrachte folgende Situation: Ein Unternehmen macht folgendes Angebot für den Verleih seiner E-Scooter:

• Die Leihgebühr beträgt 1€. Die muss man beim Ausleihen immer zahlen.
• Die Kosten für die Nutzung betragen 0.20€ pro Minute.
• Es wird genau abgerechnet. Das bedeutet, dass z.B. eine halbe Minute mit 0.10€ verrechnet wird.

Die Zuordnung "Ausleihzeit [min] -> Kosten [€]" wird mit einer Funktion $f$ beschrieben. Mit $x$ bezeichnen wir die Ausleihzeit (in min), mit $f(x)$ die zugehörigen Kosten (in €).

(a) Erstelle eine Wertetabelle, in der für mindestens 5 verschiedene $x$-Werte die zugehörigen Funktionswerte aufgelistet sind. Achte auf eine korrekte Darstellung der Wertetabelle (Anordnung und Beschriftung der Zeilen bzw. Spalten).

(b) Beschreibe die Funktion mit einem Funktionsgraph. Achte auf eine korrekte Darstellung (u.a. Wahl und Beschriftung der Achsen).

(c) Die Funktion lässt sich mit einer Funktionsgleichung vom Typ $f(x) = ...$ beschreiben. Ergänze die Funktionsgleichung. Gib auch die zur Situation passende Definitionsmenge der Funktion an.

Kontrolle

(a)

x Ausleihzeit [in min]	0	1	2	5	10
f(x) Kosten [in €]	1	1.2	1.4	2	3

(b)

Zum Herunterladen: graph_escooter.ggb

(c)
$f(x) = 1 + 0.2 \cdot x$; $x \geq 0$

Aufgabe 3 - Deutung eines Funktionsgraphen

Bei Bewegungsvorgängen interessiert man sich u.a. für die Zuordnung "Zeit [in s] -> Entfernung vom Startpunkt des Bewegungsvorgangs [in m]". Der folgende Graph verdeutlicht diese Zuordnung für ein sich bewegendes Fahrzeug.

Zum Herunterladen: s_t_diagramm.ggb

(a) Bestimme (ungefähr) die Entfernung des Fahrzeugs vom Startpunkt nach 1s bzw. 2s.

(b) Bestimme (ungefähr) die Zeit, nach der das Fahrzeug eine Entfernung von 120m vom Startpunkt erreicht hat.

(c) Bestimme (ungefähr) die Länge der Wegstrecke, die sich das Fahrzeug im Zeitintervall von 4s bis 6s weiterbewegt hat.

(d) Wahr oder falsch? Beurteile die folgenden Aussagen.

• Das Fahrzeug fährt einen Berg hinauf.
• Das Fahrzeug wird im Laufe der Zeit immer schneller.
• Das Fahrzeug fährt in der 1. Sekunde mit konstanter Geschwindigkeit.

Kontrolle

(a)
nach 1s 40m; nach 2s ca. 75m

(b)
ca 3.8s

(c)
ca 15m

(d)

• Das Fahrzeug fährt einen Berg hinauf. (Das kann man dem Diagramm nicht entnehmen.)
• Das Fahrzeug wird im Laufe der Zeit immer schneller. (falsch)
• Das Fahrzeug fährt in der 1. Sekunde mit konstanter Geschwindigkeit. (wahr)

Aufgabe 4 - Die Sprache der Mathematiker

Gegeben ist der Graph einer Funktion $f$.

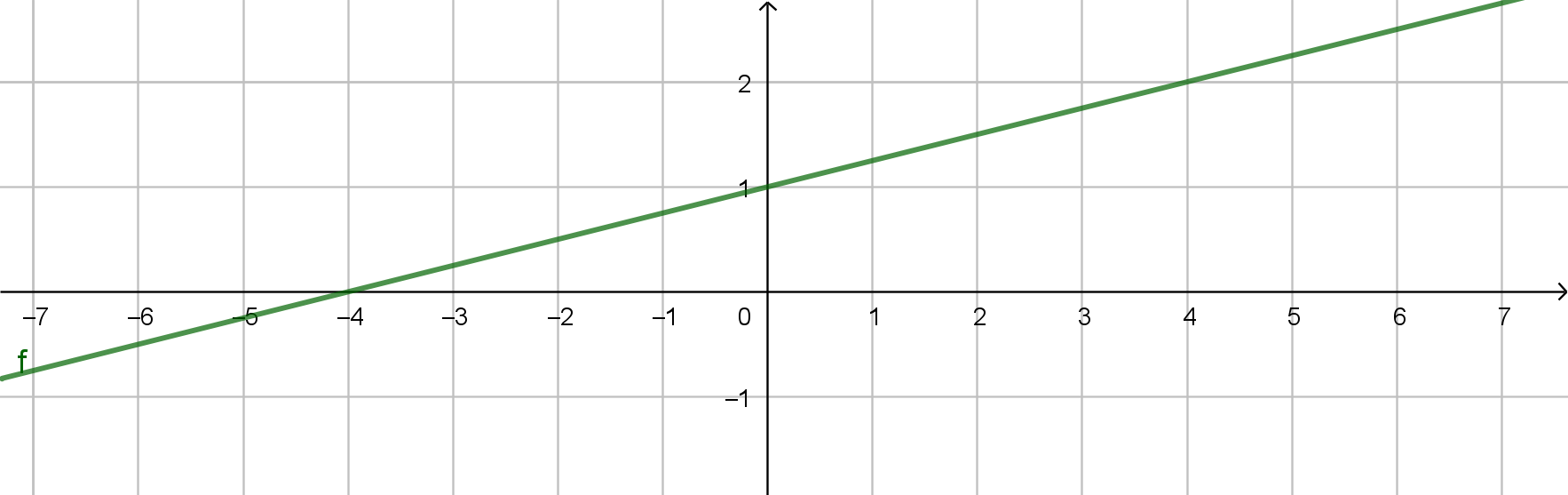
Trage in die Eingabefelder die gesuchten Werte ein. Wenn du das Ergebnis nicht weißt, dann gib ein Fragezeichen ein.

(a)	$f(0) = \;$
(b)	$f($ $) = 0$
(c)	$f: 4 \rightarrow \;$
(d)	$f(4) - f(0) = \;$
(e)	$f(3) = \;$
(f)	$f(100) = \;$