Darstellung von Funktionen

Eine neue Parkuhr testen

Das Applet simuliert die neue Parkuhr.

Zum Herunterladen: parkuhr4.ggb

Aufgabe 1

(a) Untersuche experimentell, wie sich die Parkuhr im Applet verhält. Begründe: Man kann die Zuordnung Parkzeit [in h] $\rightarrow$ Kosten [in €] bei der vorliegenden Parkuhr mit einer Funktion beschreiben.

(b) Beschreibe in Worten, wie man die Kosten für eine vorgegebene Parkzeit ermitteln kann (ohne die Parkuhr laufen zu lassen).

Eine Funktion mit einer Wertetabelle beschreiben

Die Zuordnung Parkzeit [in h] $\rightarrow$ Kosten [in €] ist bei der vorliegenden Parkuhr eindeutig. Sie ist somit eine Funktion. Wir bezeichnen diese Funktion mit $f$ und führen Schreib- und Sprechweisen für die Zuordnungen der Funktion ein.

Schreibweise	Sprechweise	Deutung im Kontext
$f: 1 \rightarrow 1.5$	Die Funktion $f$ ordnet der Ausgangszahl $1$ die Zahl $1.5$ zu.	Für die Parkzeit $1$ h ergeben sich Kosten von $1.5$ €.
$f(1) = 1.5$	Der Funktionswert an der Stelle $1$ beträgt $1.5$.	Für die Parkzeit $1$ h ergeben sich Kosten von $1.5$ €.

Beachte: Beide Schreibweisen beschreiben denselben Sachverhalt.

Zuordnungen einer Funktion kann man übersichtlich in einer Wertetabelle darstellen. Im folgenden Applet kann man eine Wertetabelle schrittweise erzeugen. In der Anleitung steht, wie man am besten vorgeht.

Anleitung zum Applet

• In der gelben Box kann man die Parkuhr für vorgegebene Parkzeiten laufen lassen. Die jeweiligen Kosten werden dann angezeigt.
• Wenn man die Kosten für eine bestimmte Parkzeit kennt (z.B. $0$ h kosten $0$ €), dann kann man die entsprechende Zuordnung (im Bsp.: $f: 0 \rightarrow 0$) in die dafür vorgesehenen Eingabefelder eintragen. Die Parkzeit wird hier auch als x-Wert bezeichnet, die zugehörigen Kosten als y-Wert bzw. Funktionswert.
• Mit der [+]-Schaltfläche wird die eingegebene Zuordnung in die Wertetabelle übertragen. Mit der [x]-Schaltfläche kann man die zuletzt übertragene Zuordnung auch wieder aus der Wertetabelle entfernen.

Zum Herunterladen: parkuhr5.ggb

Aufgabe 2

Benutze das Applet, um eine Wertetabelle für die Parkuhr-Funktion f: Parkzeit [in h] $\rightarrow$ Kosten [in €] zu erstellen. In der Wertetabelle sollen die Funktionswerte für folgende $x$-Werte stehen.

$x$	0	0.5	1	1.5	2
$f(x)$

Eine Funktion mit einem Funktionsgraph beschreiben

Zuordnungen einer Funktion kann man auch mit einem Funktionsgraph in einem Koordinatensystem veranschaulichen. Wie das geht wird im folgenden Applet verdeutlicht.

Anleitung zum Applet

• Im Applet ist bereits eine Wertetabelle mit Zuordnungen vorgegeben.
• Die Zuordnungen sollen im Koordinatensystem veranschaulicht werden. Man kann hierzu die Zuordnungspfeile mit Hilfe von beweglichen Punkten passend einstellen.
• Mit [Kontrolle] kann man den Funktionsgraph einblenden.

Zum Herunterladen: parkuhr6.ggb

Aufgabe 3

(a) Benutze das Applet, um die Zuordnungen aus der vorgegebenen Wertetabelle im Koordinatensystem zu veranschaulichen. Bewege hierzu die beweglichen Punkte so, dass die Pfeile von den betrachteten $x$-Werten zu den passenden $y$-Werten führen. Kontrolliere deine Ergebnisse.

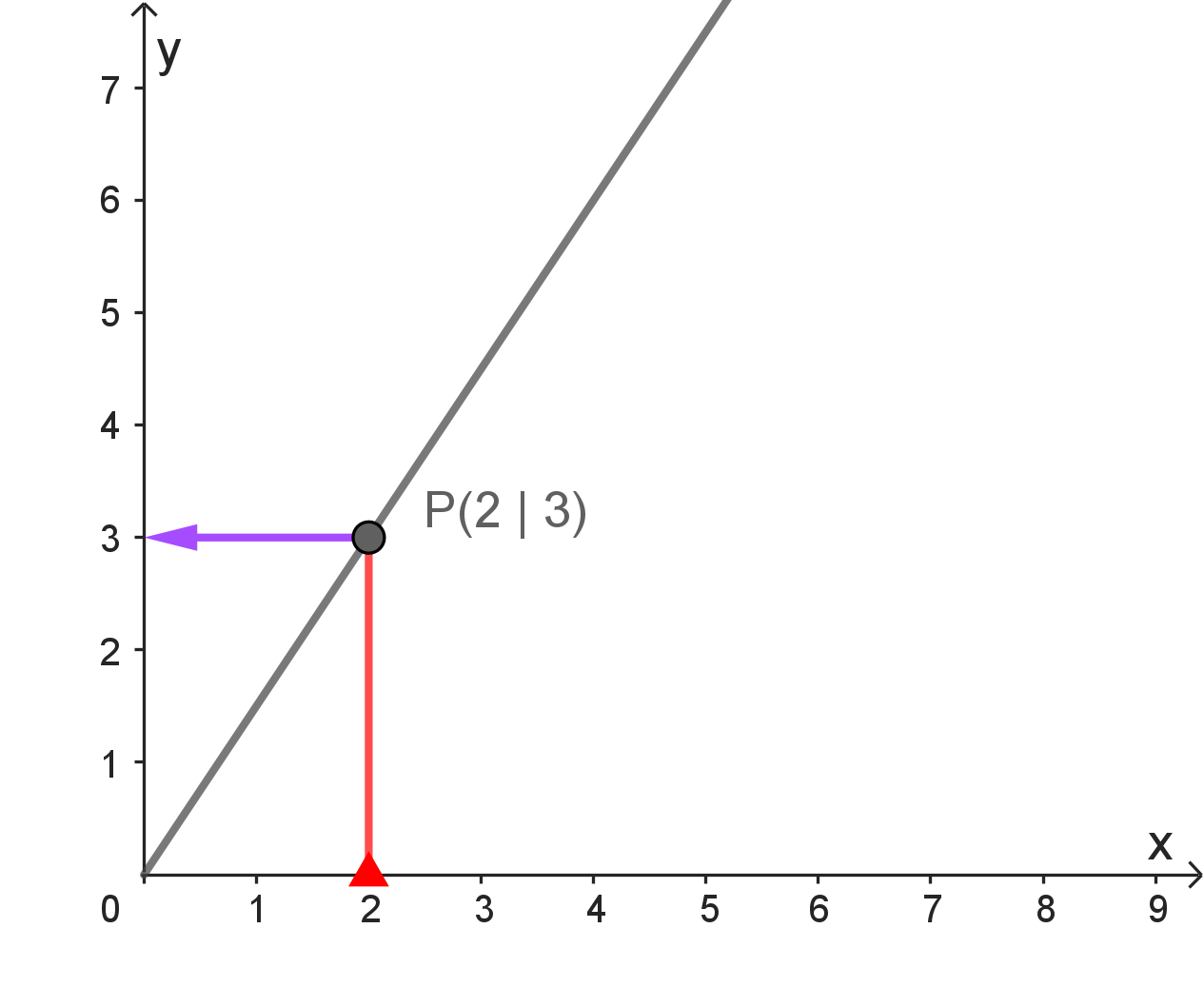
(b) Ergänze: Die Zuordnung $f: 2 \rightarrow 3$ kann man mit Hilfe des Punktes $P(\dots|\dots)$ verdeutlichen.

(c) Nutze den mit der [Kontrolle] eingeblendeten Funktionsgraph, um die Kosten für eine Parkzeit von $3.5$ [h] abzuschätzen. Bewege hierzu einen Pfeil an die passenden Positionen.

Eine Funktion mit einer Funktionsgleichung beschreiben

Die bisher betrachteten Darstellungsmöglichkeiten haben den Nachteil, dass sie die Gesamtheit aller Zuordnungen einer Funktion meist nicht erfassen. Um eine Funktion (mit all ihren Zuordnungen) präzise zu beschreiben, verwendet man eine algebraische Darstellung mit einer Funktionsgleichung. Wie das geht wird im folgenden Applet verdeutlicht.

Anleitung zum Applet

• Im Applet ist bereits eine Wertetabelle mit Zuordnungen vorgegeben.
• Die Zuordnungen sollen mit einer Funktionsgleichung beschrieben werden. Hierzu muss man im Eingabefeld für $f(x)$ die passende Formel ergänzen.
• Die Funktionsgleichung kann man überprüfen, indem man im Eingabefeld links neben der Funktionsgleichung $x$-Werte vorgibt. Es sollten dann jeweils korrekt Funktionswerte rechts neben der Funktionsgleichung angezeit werden.

Zum Herunterladen: parkuhr7.ggb

Aufgabe 4

(a) Überlege dir zunächst, wie du rechnerisch die Kosten für eine Parkzeit wie z.B. $5$ h bestimmen kannst.

(b) Verallgemeinere die Überlegungen. Beschreibe mit einer Formel, wie man die Kosten für eine Parkzeit von $x$ [h] bestimmen kann. Trage diese Formel in das Eingabefeld für $f(x)$ ein. Du hast dann die Funktionsgleichung für die Funktion $f$ festgelegt.

(c) Überprüfe die Funktionsgleichung, indem du $x$-Werte in das Eingabefeld links neben der Funktionsgleichung vorgibst. Die Funktionswerte werden dann mit Hilfe der Funktionsgleichung bestimmt und rechts neben der Funktionsgleichung angezeigt. Wenn du immer korrekte Funktionswerte erhältst, dann stimmt die Funktionsgleichung.

Aufgabe 5

In den vorangehenden Aufgaben hast du die Funktion zur Beschreibung des Parkuhrverhaltens auf vier verschiedene Weisen dargestellt:

• verbal mit der Umgangssprache
• exemplarisch mit einer Wertetabelle
• geometrisch mit einem Funktionsgraph
• algebraisch mit einer Funktionsgleichung

Erläutere kurz die Vor- und Nachteile dieser Darstellungsmöglichkeiten.

Zusammenfassung

Zusammenfassung

Verbale Beschreibung einer Funktion

Mit einer verbalen Beschreibung versucht man, das Verhalten einer Funktion mit eigenen Worten zu beschreiben.

Beispiel

Die Funktion ordnet einer Parkzeit [in h] die Kosten [in €] zu. Die Kosten betragen dabei $1.5$ € pro Stunde. Dabei wird zeitgenau abgerechnet. Für z.B. $2.5$ Studen muss man $4.25$ € zahlen.

Vorteil einer verbalen Funktionsbeschreibung:
Man kann die Beschreibung sehr flexibel gestalten.

Nachteil einer verbalen Funktionsbeschreibung:
Die Beschreibung wird ggf. nicht richtig verstanden.

Wertetabelle einer Funktion

Mit einer Wertetabelle beschreibt man Zuordungen einer Funktion tabellarisch. Man gibt (frei wählbare) $x$-Werte vor und bestimmt die zugeordneten $y$-Werte bzw. Funktionswerte und listet sie in einer Tabelle auf.

Beispiel

$x$	0	1	2	3	4
$f(x)$	0	1.5	3	4.5	6

Vorteil einer Funktionsdarstellung mit einer Wertetabelle:
Zuordnungen sind direkt ablesbar.

Nachteil einer Funktionsdarstellung mit einer Wertetabelle:
Es werden nur wenige Zuordnungen dargestellt. Man gewinnt hierdurch oft keinen gesicherten Einblick in die Gesamtheit aller Zuordnungen der Funktion.

Funktionsgraph

Mit einem Funktionsgraph beschreibt man Zuordungen einer Funktion in einem Koordinatensystem. Jede Zuordnung der Gestalt $x \rightarrow y$ wird mit einem Punkt $(x | y)$ verdeutlicht. Die Zuordnung führt von einer Stelle der $x$-Achse über den Punkt $(x | y)$ zu einer Stelle auf der $y$-Achse.

Beispiel

Vorteil einer Funktionsdarstellung mit einem Graph:
Man gewinnt – zumindest im dargestellen Bereich – einen guten Überblick über die Zuordnungen.

Nachteil einer Funktionsdarstellung mit einer Wertetabelle:
Man kann einzelne Zuordnungen am Graph oft nur näherungsweise ablesen.

Funktionsgleichung

Mit einer Funktionsgleichung kann man die Gesamtheit der Zuordungen einer Funktion algebraisch beschreiben.

Beispiel

$f(x) = 1.5x$; $x \geq 0$

Wenn man für $x$ einen Wert aus der Definitionsmenge (hier: eine reelle Zahl, die größer oder gleich $0$ ist) in den Term auf der rechten Seite der Gleichung einsetzt, dann erhält man den Funktionswert, der dem Ausgangswert $x$ zugeordnet ist.

Es gilt: $f(2) = 1.5 \cdot 2 = 3$

Also: $f: 2 \rightarrow 3$

Vorteil einer Funktionsdarstellung mit einer Gleichung:
Die Zuordnungen der Funktion sind präzise festgelegt. Man kann alle Zuordnungen rechnerisch bestimmen.

Nachteil einer Funktionsdarstellung mit einer Gleichung:
Die Darstellung ist eher abstrakt. Man benötigt ein gutes Termverständnis, um sich eine Vorstellung über die Gesamtheit der Zuordnungen zu machen.

Zusammenfassung als Video