Eigenschaften von Funktionen
Zielsetzung
Funktionen sind mathematische Objekte, die Eigenschaften haben.
Diese Sichtweise steht hier im Vordergrund.
Wenn du die in den vorangehenden Abschnitten thematisierten Aspekte des Funktionskonzepts sicher beherrschst,
dann bearbeite die folgenden Aufgaben.
Eigenschaften von Funktionen bestimmen
In den folgenden Aufgaben sind jeweils mehrere Funktionen gegeben.
Untersuche, ob die Funktionen die mit A, B und C gekennzeichneten Eigenschaften haben.
Trage in die Eingabefelder w (für wahr) oder f (für falsch) ein.
Noch wichtiger als das korrekte Ergebnis ist die Erklärung, warum das so ist.
Begründe also jeweils deine Aussagen.
Aufgabe 1
Die Funktionen, die hier betrachtet werden, sind mit einer Wertetabelle dargestellt.
- A: $f(2) = 4$
- B: $f(x) > 0$ für alle $x \geq 0$
- C: $f(2x) = 2f(x)$ für alle $x \geq 0$
| Wertetabelle |
A (w/f) |
B (w/f) |
C (w/f) |
| $x$ |
0 |
1 |
2 |
3 |
4 |
| $f(x)$ |
0 |
2 |
4 |
6 |
8 |
|
|
|
|
| $x$ |
0 |
1 |
2 |
3 |
4 |
| $f(x)$ |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
| $x$ |
0 |
1 |
2 |
3 |
4 |
| $f(x)$ |
0 |
0.5 |
1 |
1.5 |
2 |
|
|
|
|
Aufgabe 2
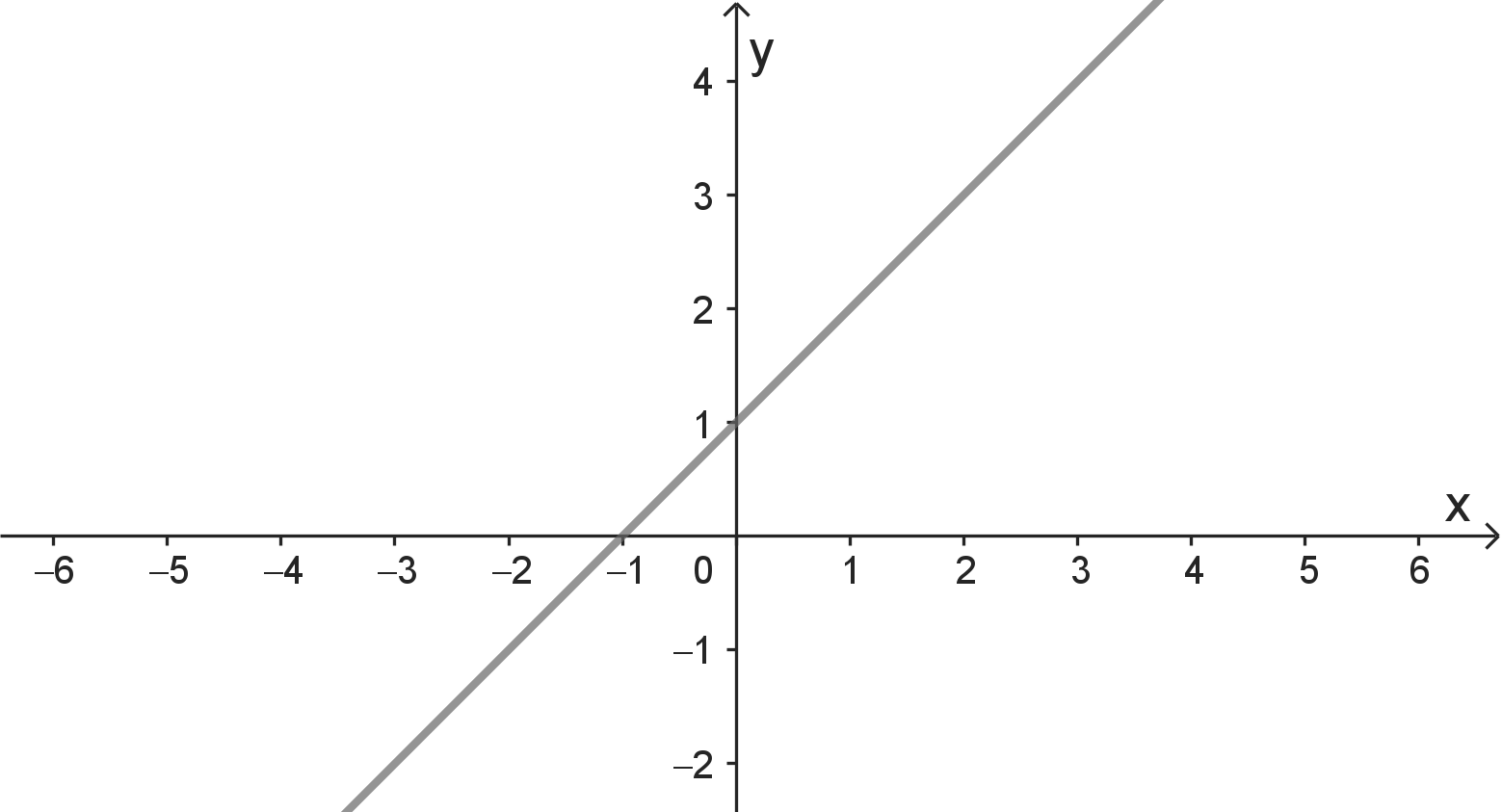
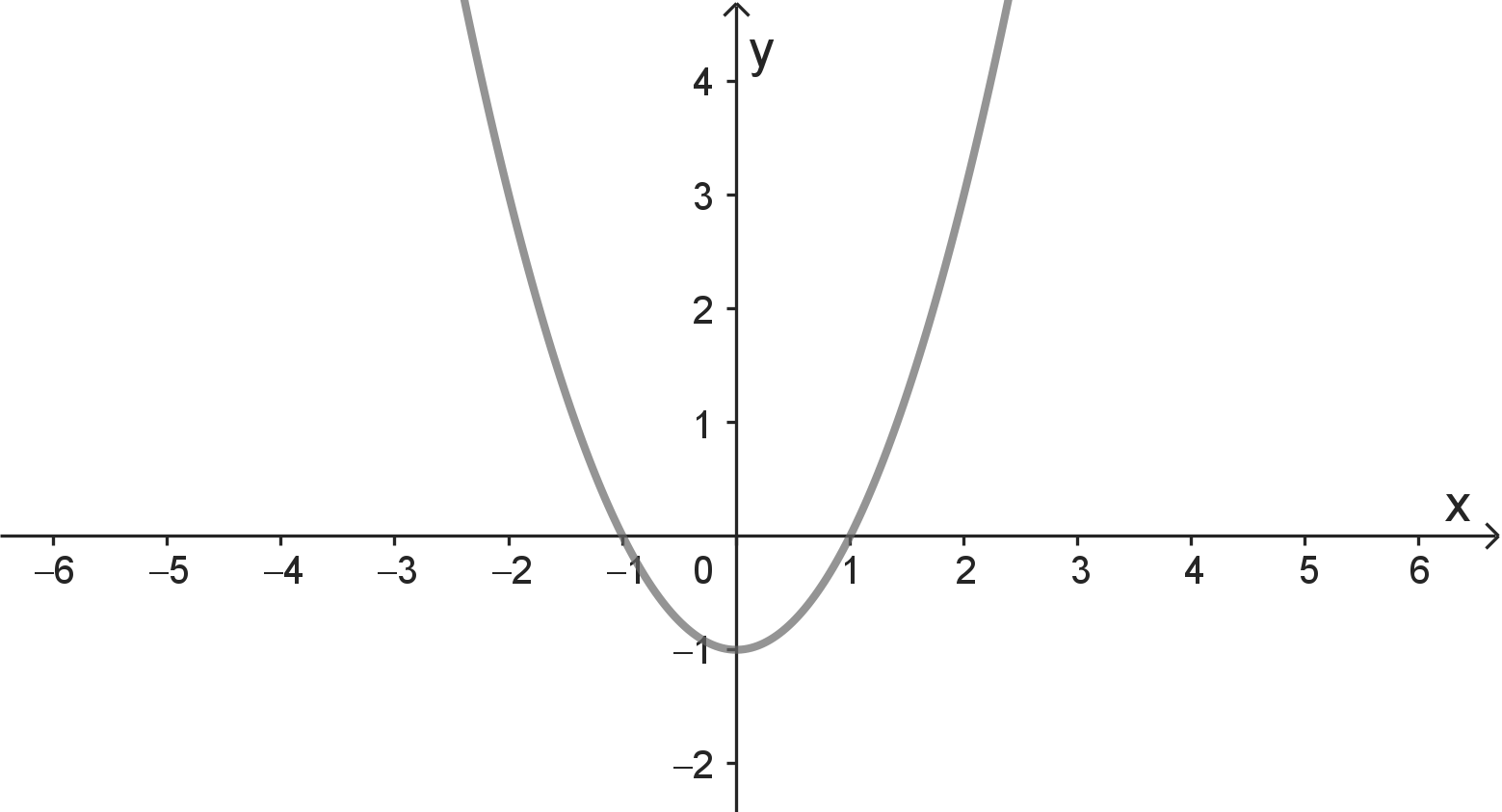
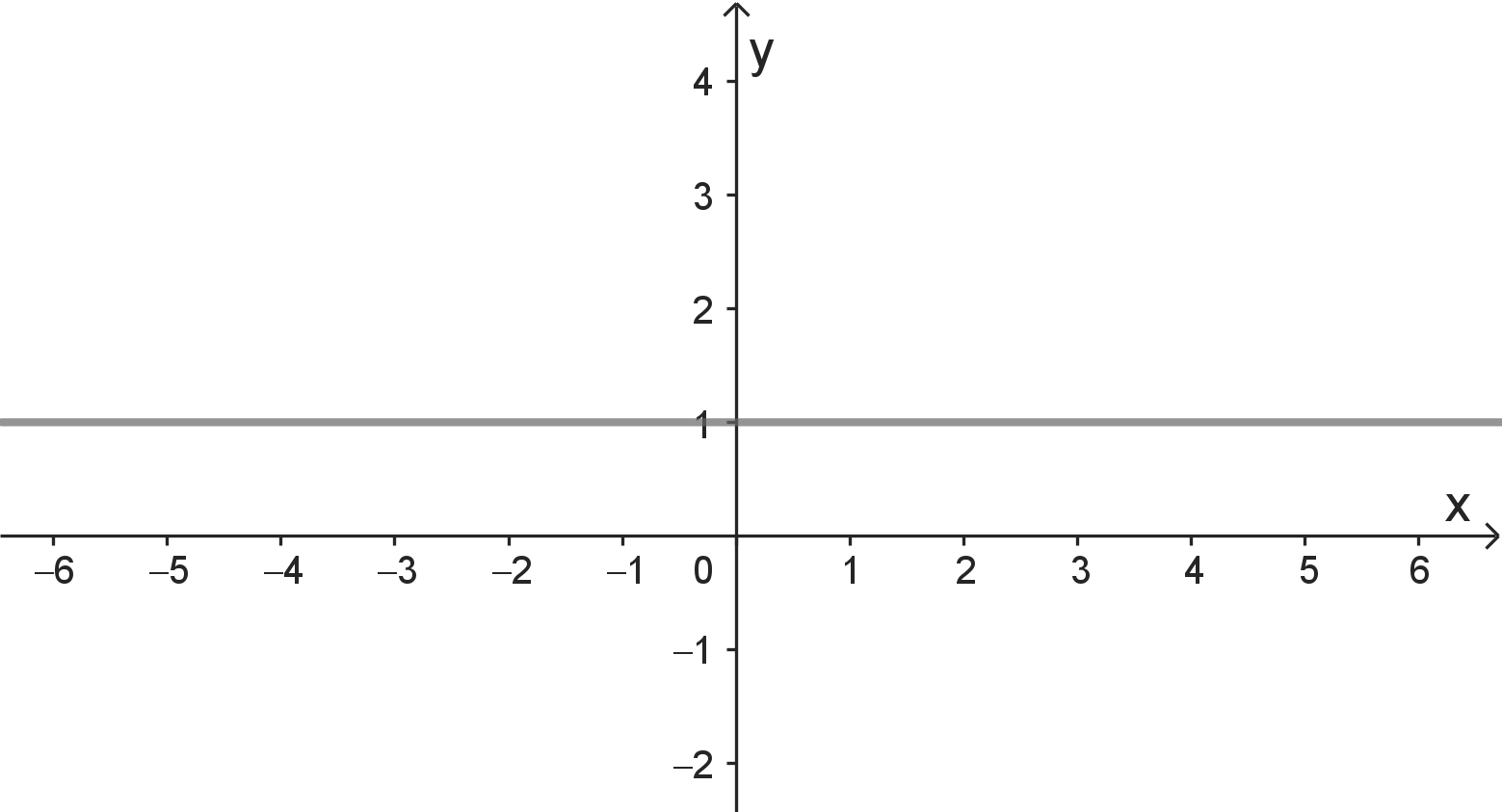
Die Funktionen, die hier betrachtet werden, sind mit einem Funktionsgraph dargestellt.
- A: $f(1) = 0$
- B: $f(x) > 0$ für alle reellen Zahlen $x$
- C: $f(x+1) \geq f(x)$ für alle reellen Zahlen $x$
| Funktionsgraph |
A (w/f) |
B (w/f) |
C (w/f) |
|
|
|
|
|
|
|
|
|
|
|
|
Aufgabe 3
Die Funktionen, die hier betrachtet werden, sind mit einer Funktionsgleichung dargestellt.
- A: $f(0) = 0$
- B: $f(x) \geq 0$ für alle reellen Zahlen $x$
- C: $f(-x) = f(x)$ für alle reellen Zahlen $x$
| Funktionsgleichung |
A (w/f) |
B (w/f) |
C (w/f) |
|
$f(x) = 1$
|
|
|
|
|
$f(x) = x$
|
|
|
|
|
$f(x) = 0.5 x^2$
|
|
|
|




