Funktion als Zuordnung
Aufgabe 1
Welche der folgenden Zuordnungen aus dem Alltag sind eindeutige Zuordnungen? Begründe (ggf. mit einem Pfeildiagramm).
- Person $\rightarrow$ Geburtsjahr
- Person $\rightarrow$ Telefonnummer
- Wort $\rightarrow$ Anzahl der Buchstaben und Zeichen
- Wort $\rightarrow$ Bedeutung
- Preis $\rightarrow$ Lebensmittel in einem Geschäft
- Lebensmittel in einem Geschäft $\rightarrow$ Preis
Aufgabe 2
Welche der folgenden Wertetabellen gehören nicht zu Funktionen? Begründe.
| $x$ | -2 | -1 | 0 | 1 | 2 |
| $f(x)$ | 2 | 1 | 0 | -1 | -2 |
| $x$ | -2 | -1 | 0 | 1 | 2 |
| $f(x)$ | 0 | 0 | 0 | 0 | 0 |
| $x$ | 0 | 0 | 0 | 0 | 0 |
| $f(x)$ | -2 | -1 | 0 | 1 | 2 |
| $x$ | 2 | 1 | 0 | 1 | 2 |
| $f(x)$ | 0 | 0 | 0 | 0 | 0 |
Aufgabe 3
(a) Welche der folgenden Graphen gehören zu Funktionen? Verdeutliche mit Hilfe der beweglichen Zuordnungspfeile im Applet.
Zum Herunterladen: graphen.ggb
(b) Formuliere eine Regel, mit der man entscheiden kann, ob ein Graph zu einer Funktion gehört.
Aufgabe 4
Die Abbildung zeigt (ausschnittsweise) Zuordnungen einer Funktion.
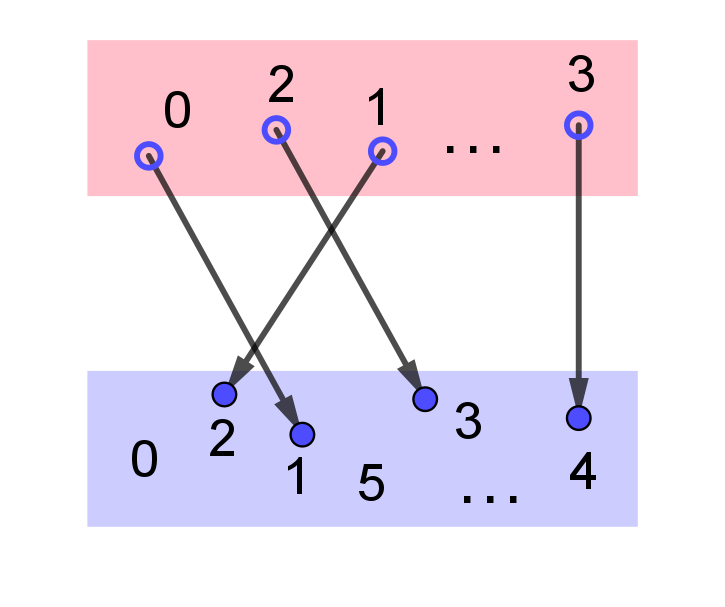
(a) Teste in den Applets, welche Gleichung die Funktion korrekt beschreibt. Gib hierzu passende Zahlen in das Eingabefeld links neben der grünen Box ein und beobachte die zugeordneten Zahlen rechts neben der grünen Box.
| Funktionsgleichung | Funktions- bezeichner |
Variablen- bezeichner |
|---|---|---|
| $f$ | $x$ | |
| $g_2$ | $x$ | |
| $K$ | $t$ | |
| $x$ |
(b) Die Funktionsbeschreibungen mit einer Funktionsgleichung unterscheiden sich in der Wahl des Funktionsbezeichers und des Variablenbezeichners. Welche Schlussfolgerung kann man aus Aufgabenteil (a) ziehen? Formuliere eine Regel.

