Füllgraphen
Zur Orientierung
Hier geht es um Zuordnungen, die beim Füllen einer Vase eine Rolle spielen. Wir betrachten die Füllvorgänge dabei aus zwei unterschiedlichen Perspektiven.
Aufgabe 1: Füllhöhe $\rightarrow$ Füllvolumen
Im Applet unten siehst du links eine 8cm hohe Vase und rechts einen Füllgraphen. Die Form der Vase kannst du anpassen, indem du die vier Punkte E0, E1, E2 und E3 verschiebst. Den Wasserstand kannst du durch Verschieben des Punktes W regulieren
(a) Erkunde das Applet, indem du die Punkte E0, E1, E2, E3 und W veränderst. Was zeigt der sogenannte Füllgraph an?
Zum Herunterladen: fuellgraph-vase2.ggb
(b) Probiere aus, wie der Füllgraph aussieht, wenn die Vase nach innen gewölbt bzw. nach außen gewölbt ist. Erkläre den Zusammenhang.
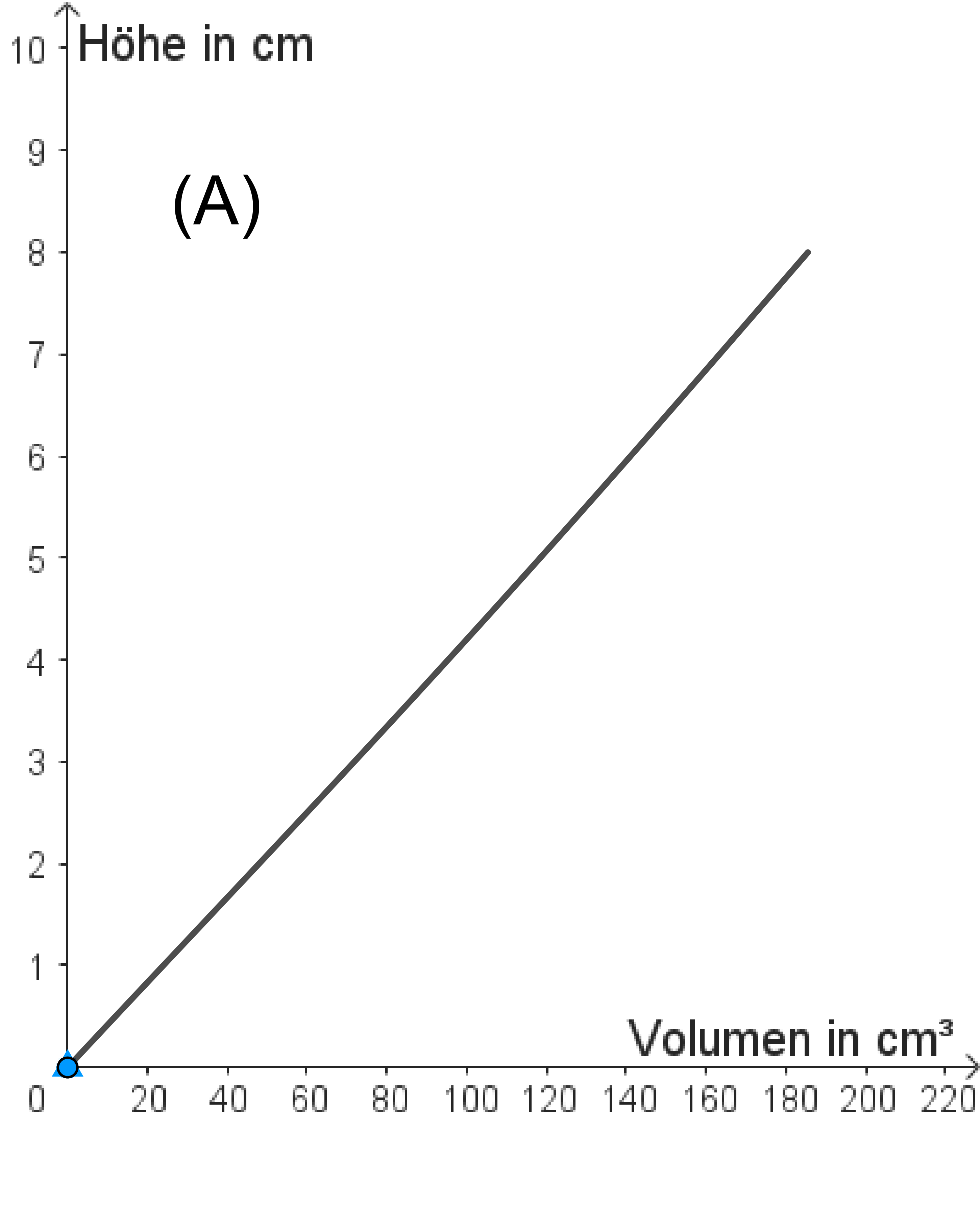
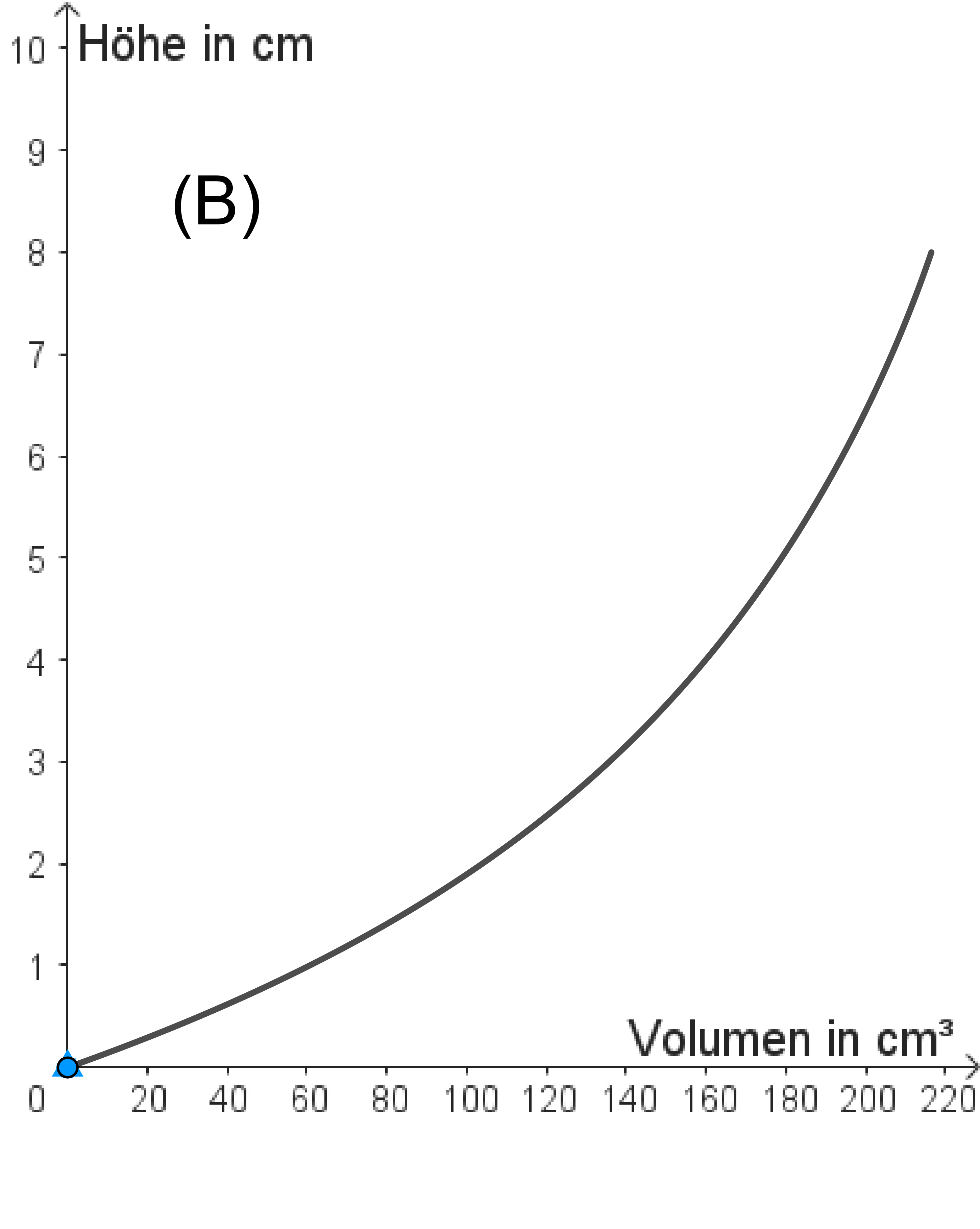
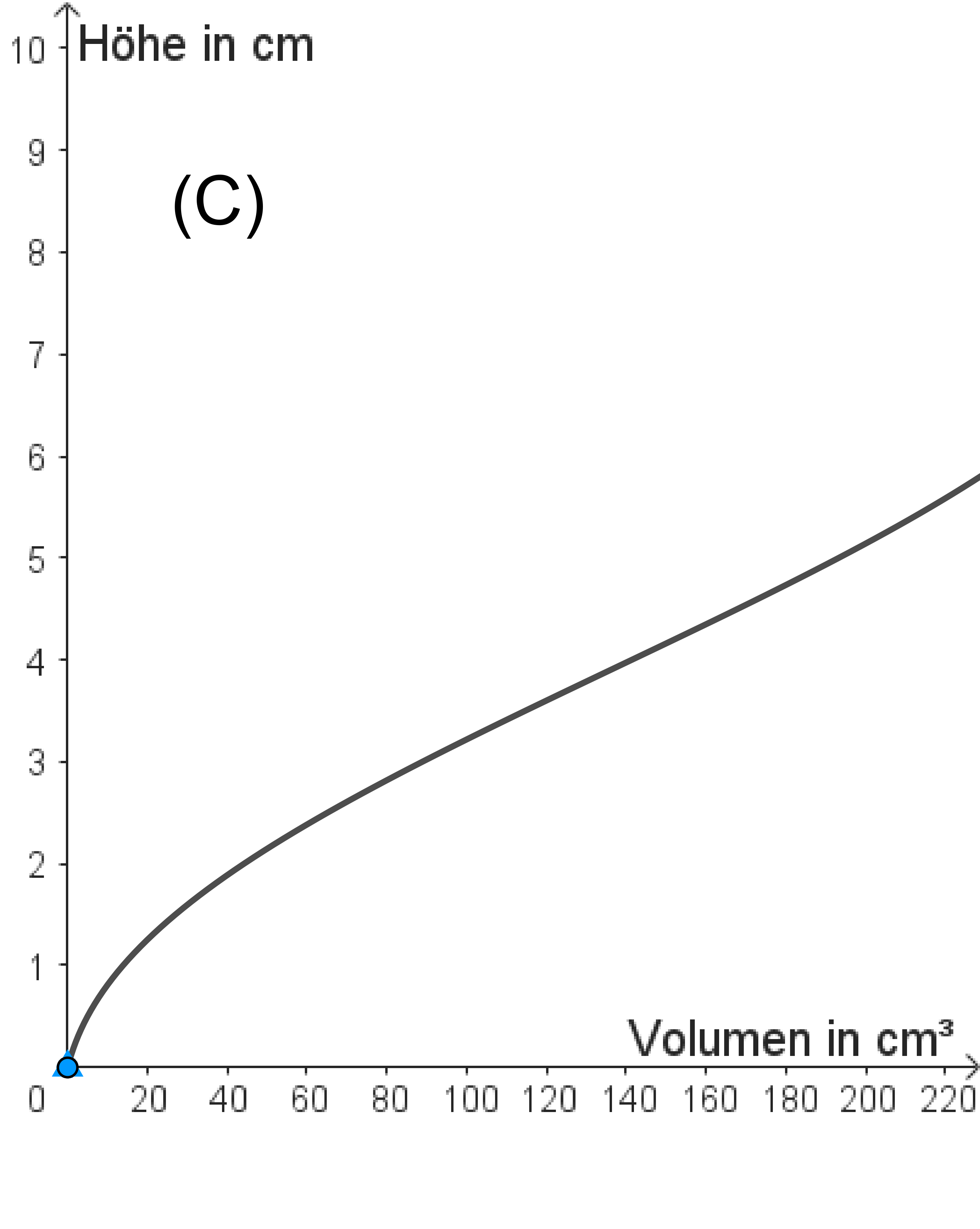
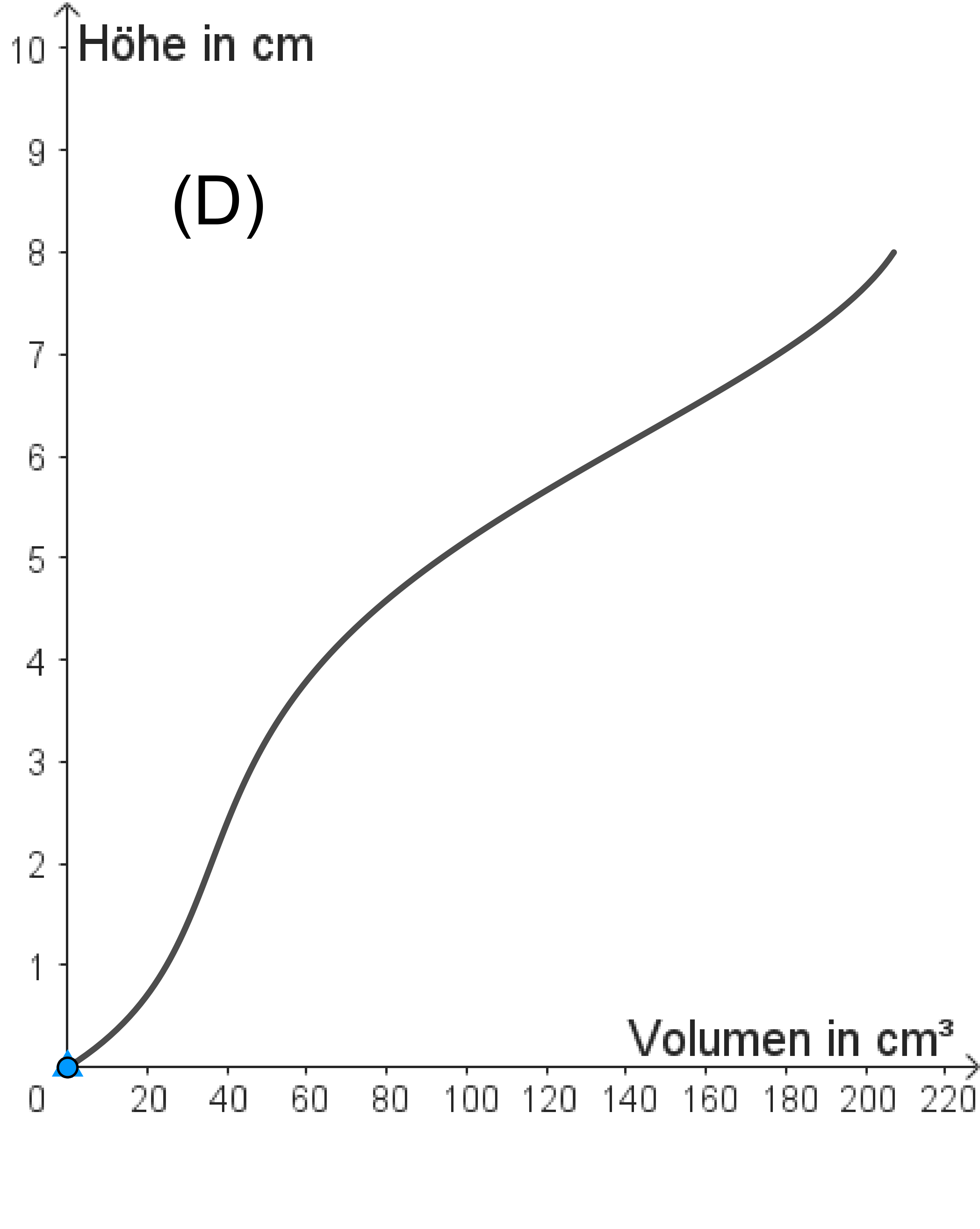
(c) Hier siehst du vier Füllgraphen (A) bis (D). Töpfere im Applet jeweils die passende Vase durch Verschieben der Punkte E0, E1, E2 und E3.
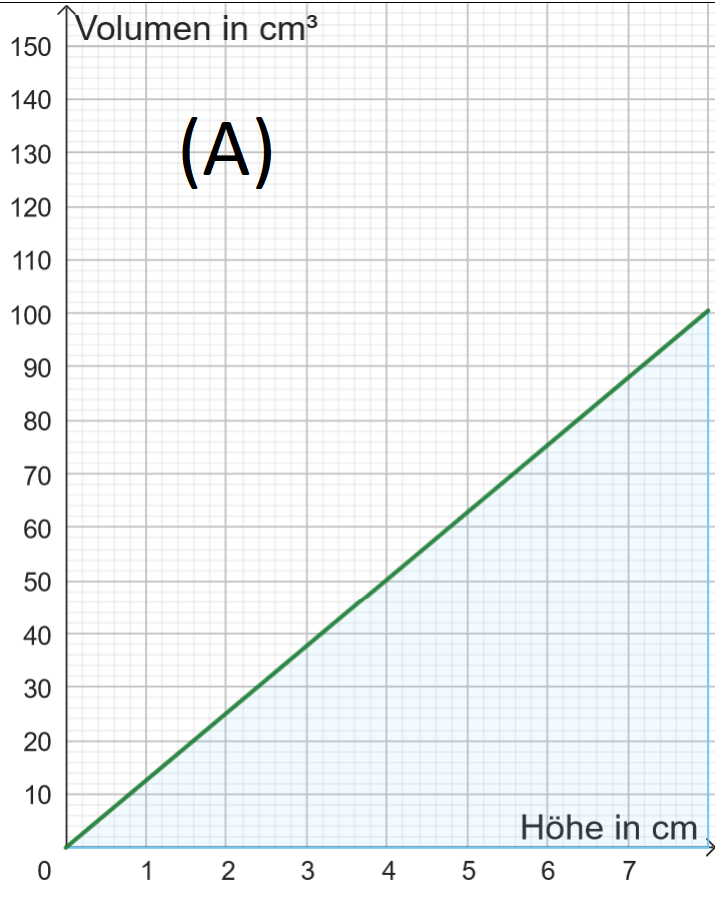
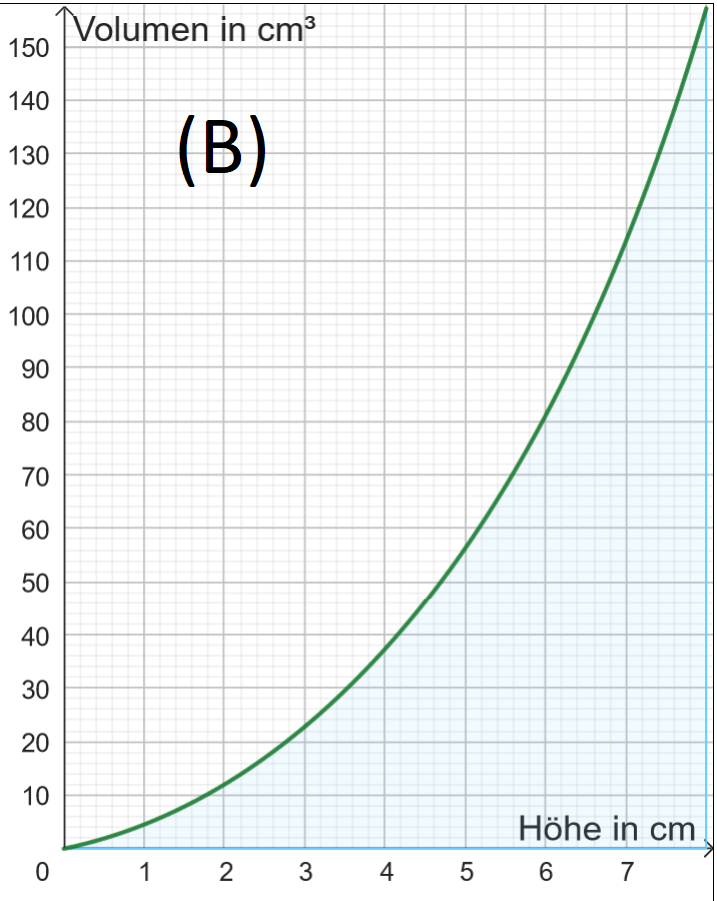
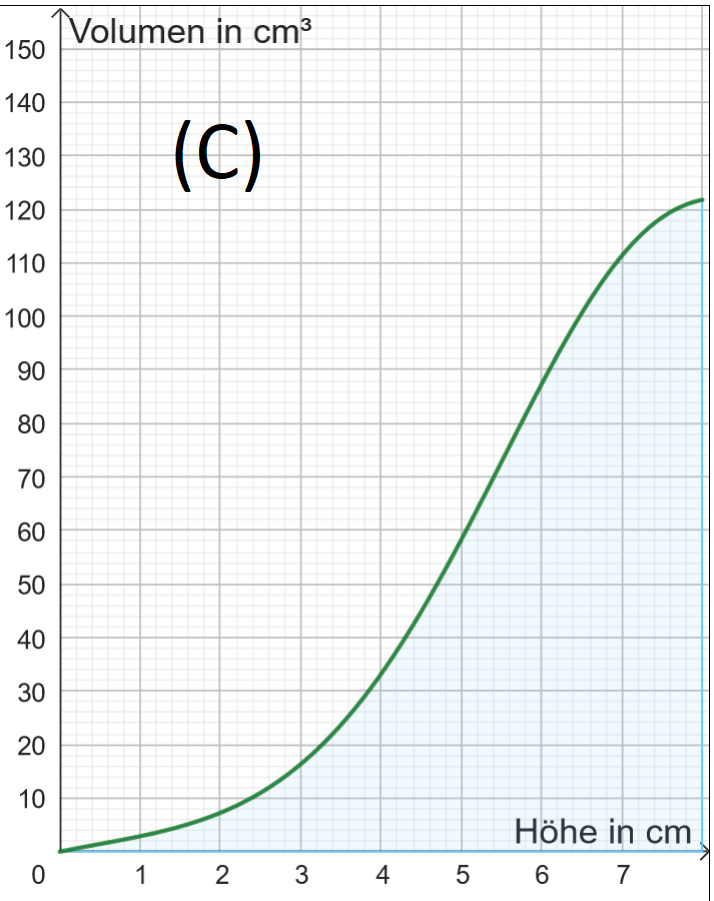
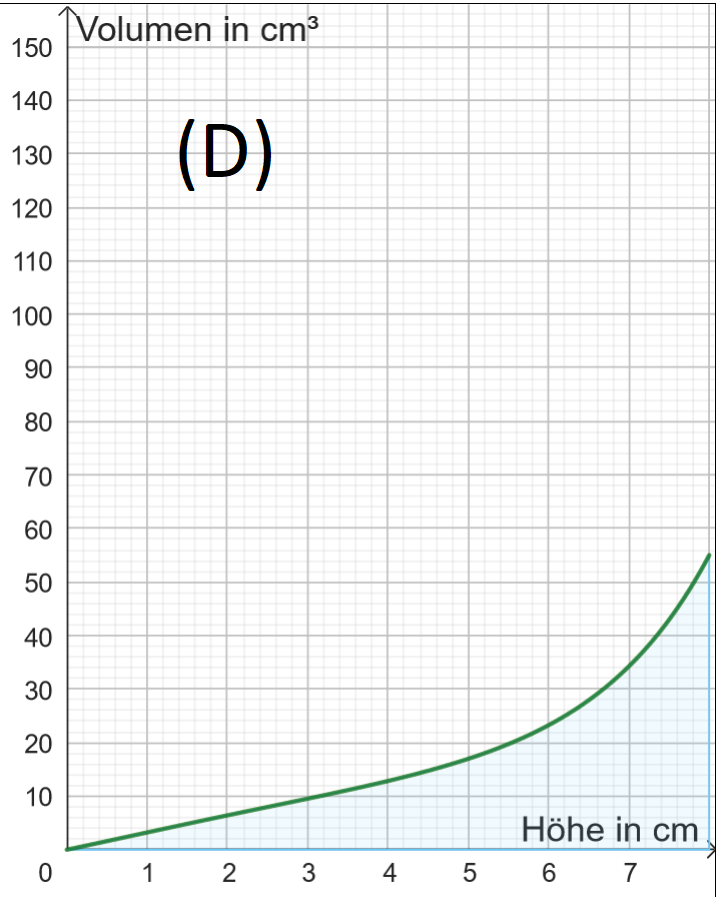
Aufgabe 2: Füllvolumen $\rightarrow$ Füllhöhe
Im Applet unten siehst du links eine 8cm hohe Vase und rechts einen Füllgraphen. Die Form der Vase kannst du anpassen, indem du die vier Punkte E0, E1, E2 und E3 verschiebst. Mit dem blauen Zeiger auf der Volumenachse im Koordinatensystem kann du jetzt Wasser in die Vase füllen. Du muss hierzu den Zeiger nur nach rechts bewegen.
(a) Erkunde das Applet, indem du die Punkte E0, E1, E2, E3 und W veränderst. Was zeigt der sogenannte Füllgraph an?
Zum Herunterladen: fuellgraph-vase7.ggb
(b) Probiere aus, wie der Füllgraph aussieht, wenn die Vase nach innen gewölbt bzw. nach außen gewölbt ist. Erkläre den Zusammenhang.
(c) Hier siehst du vier Füllgraphen (A) bis (D). Töpfere im Applet jeweils die passende Vase durch Verschieben der Punkte E0, E1, E2 und E3.