Einstieg - Von der Intuition zur Präzision
Das Ziel klären
Über viele Jahrhunderte haben Mathematiker mit einem intuitiven Grenzwertverständnis gearbeitet und damit komplexe mathematische Zusammenhänge erschlossen.
So war schon im Altertum bekannt, dass die Folge $\left( a_n \right)$ mit
$a_1 = \frac{1}{2}$
$a_2 = \frac{1}{2} + \frac{1}{4}$
$a_3 = \frac{1}{2} + \frac{1}{4} + \frac{1}{8}$
$a_4 = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16}$
...
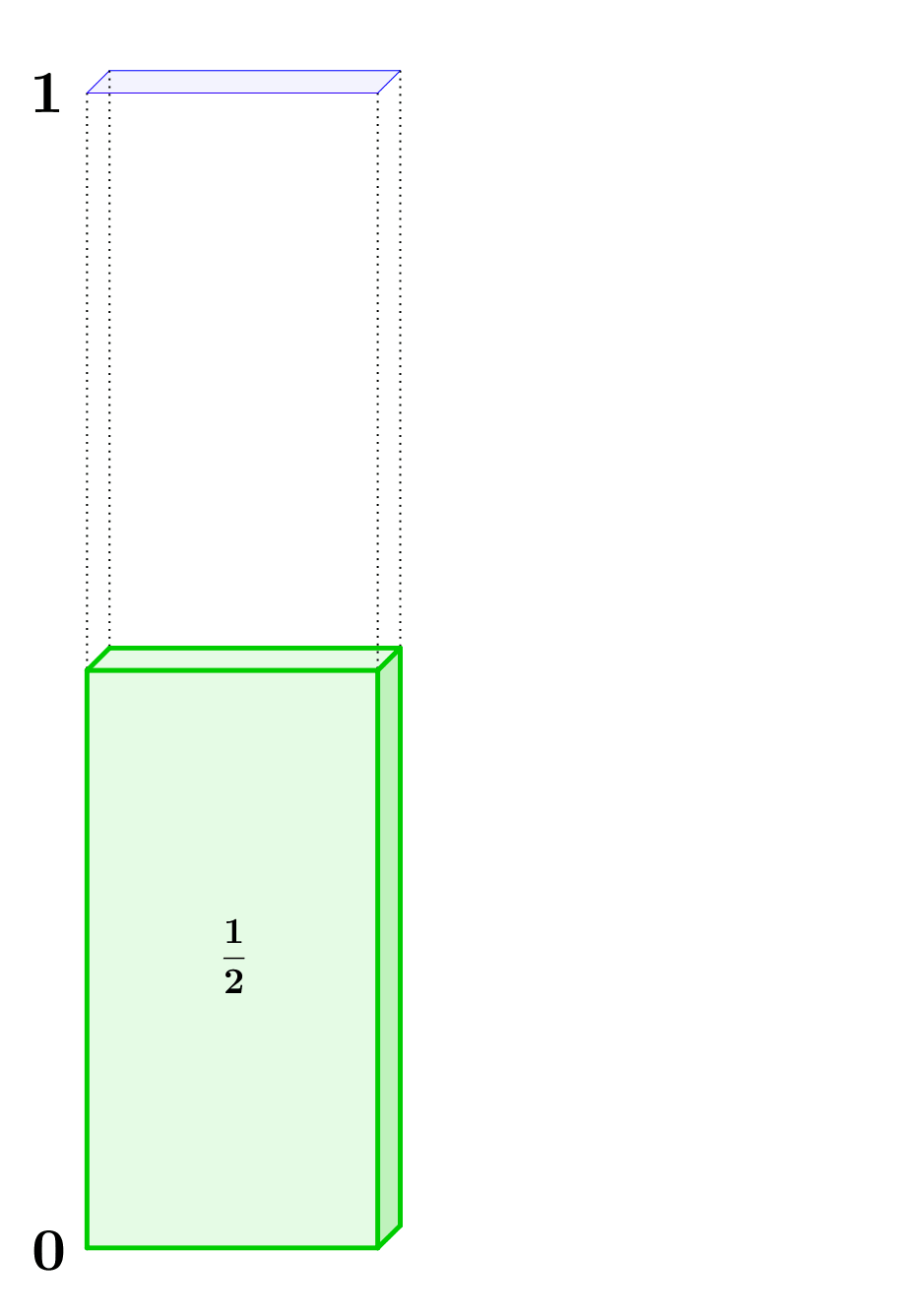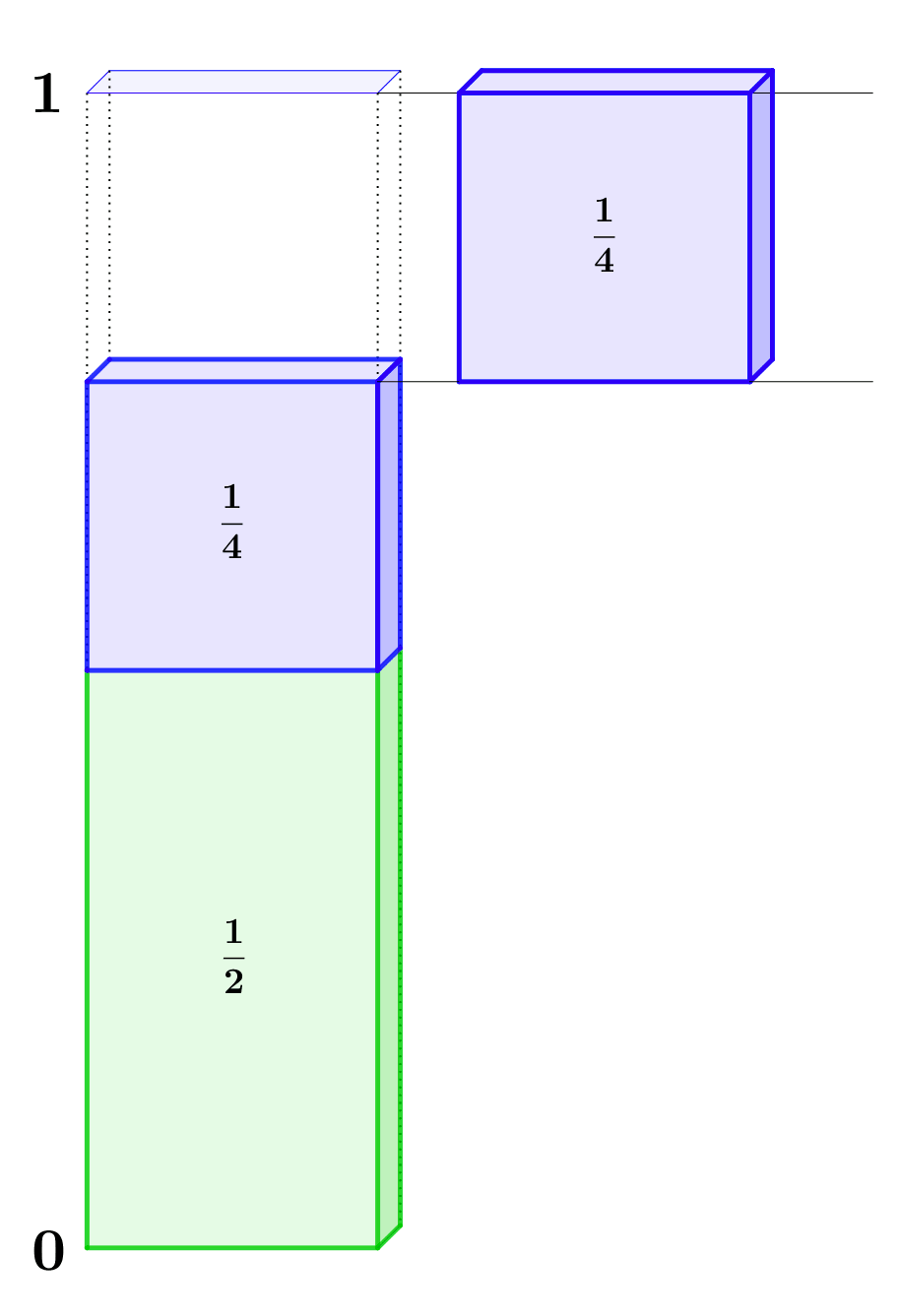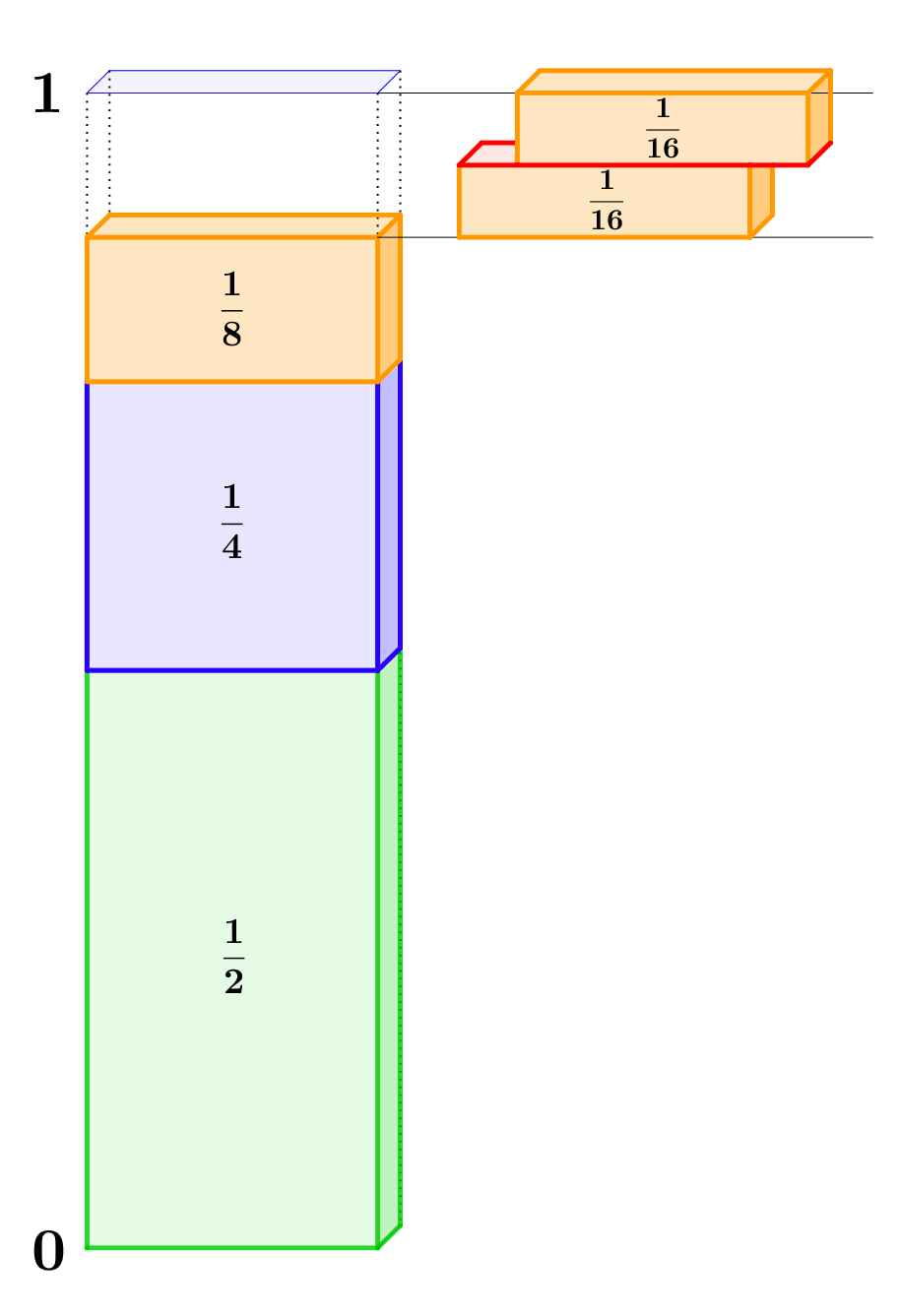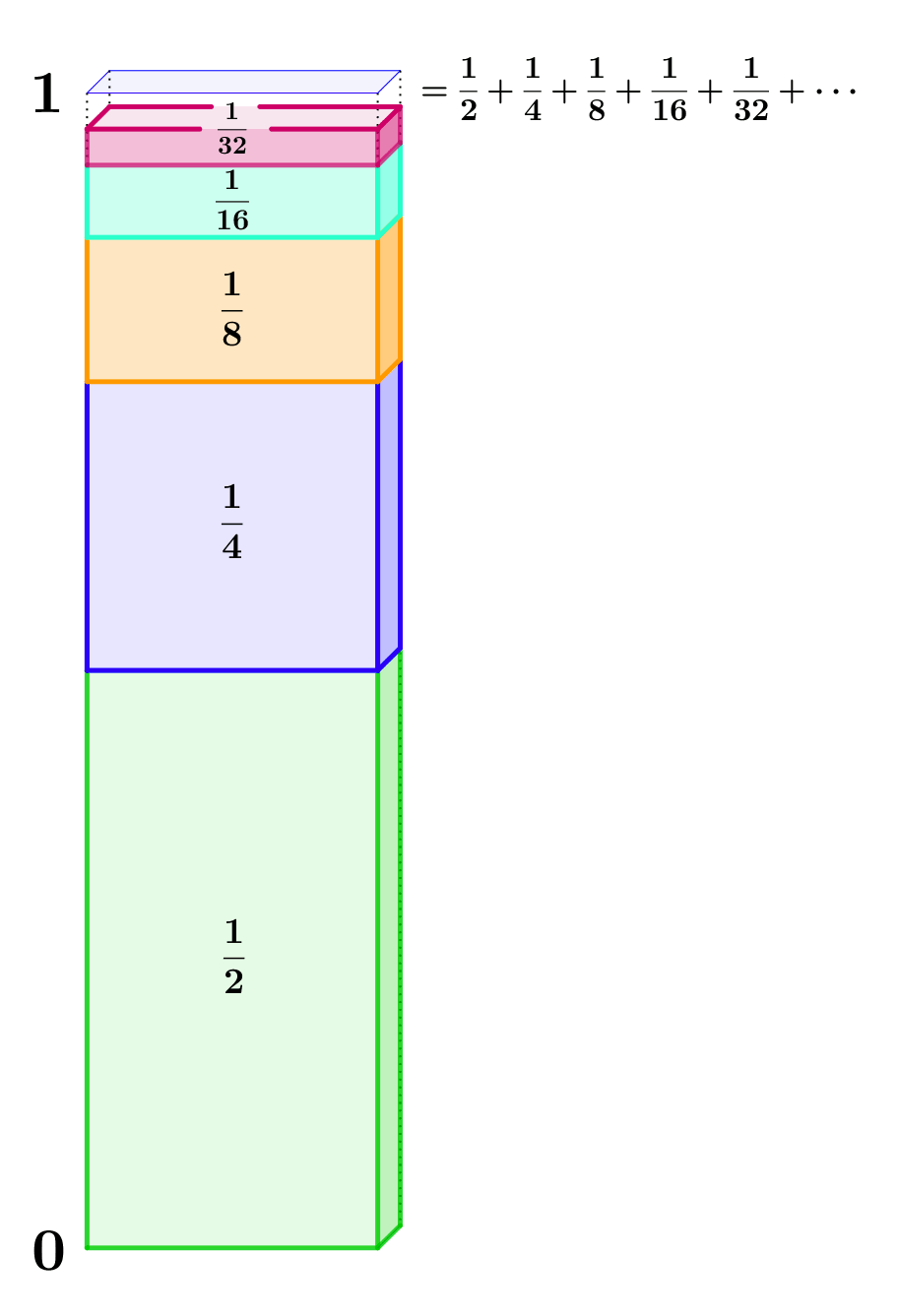
den Grenzwert $1$ hat.
Die folgende Animation verdeutlicht, wie man sich diesen Zusammenhang klarmachen kann.
Aufgabe 1
Erkläre mit Hilfe der Animation, warum die oben beschriebene Folge den Grenzwert $1$ hat. Erläutere kurz, warum die Animation noch keinen Beweis für den Zusammenhang liefert.
Zielsetzung
Erst im 19. Jahrhundert ist das Bedürfnis entstanden, den Grenzwertbegriff präzise zu erfassen. Man hat erkannt, dass ein intuitiver Grenzwertgegriff nicht ausreicht, um mathematische Problemstellungen zweifelsfrei zu klären. Gegen Ende des 19. Jahrhundert wurde der Begriff dann von dem Mathematiker Weierstraß präzise definiert – so wie er auch heute noch benutzt wird.
Ziel der folgenden Abschnitten ist es, diesen Weg von den Unzulänglichkeiten eines intuitiven Grenzwertbegriffs hin zu den Vorzügen einer präzisen Grenzwertdefinition zu skizzieren.
Quellen
- [1]: Geometrische Reihe - Urheber: Petrus3743 - Lizenz: Creative Commons BY-SA 4.0