Vertiefung
Zur Orientierung
Im letzten Abschnitt hast du bereits Grenzwerte von Funktionen für $x \rightarrow +\infty$ und $x \rightarrow -\infty$ bestimmt. Wir sind dort von einem intuitiven Grenzwertverständnis ausgegangen. In diesem Abschnitt holen wir eine präzise Festlegung des Grenzwertbegriff bei Funktionen nach.
Eine Definition entwickeln
Im letzten Abschnitt hast du folgende Grenzverhaltenssituationen betrachtet.
| Situation | Grenzverhalten |
|---|---|
|
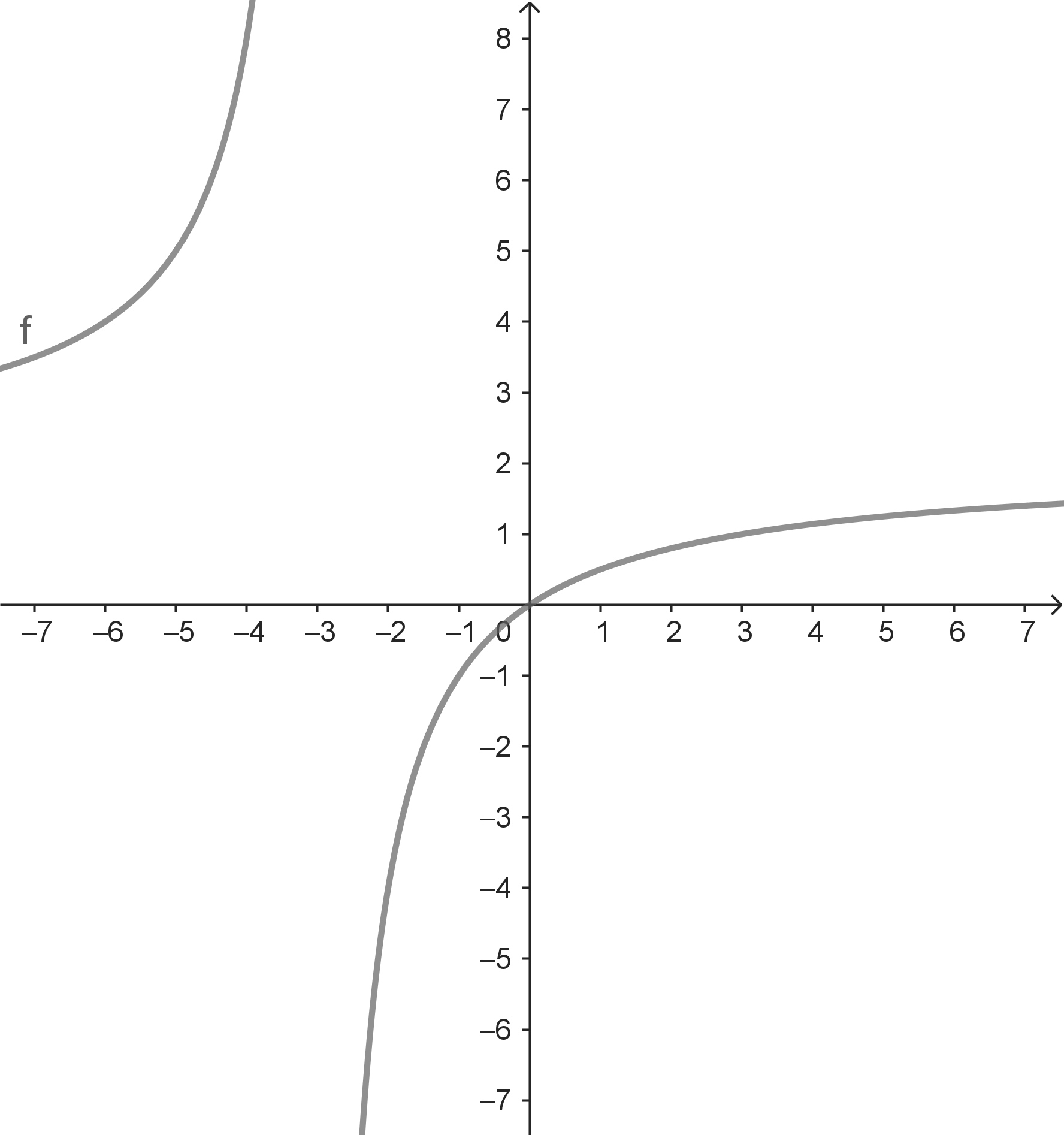
Die Funktionswerte $f(x)$ stabilisieren sich für $x \rightarrow +\infty$ (bzw. für $x \rightarrow -\infty$) bei der Zahl $g = 2$.
Das siehtman, wenn man eine $x$-Werte-Folge $(x_n)$ mit $x_n \rightarrow +\infty$ (bzw. für $x \rightarrow -\infty$) durchläuft und dabei die Folge $(f(x_n))$ der zugehörigen Funktionswerte betrachtet. Dabei ist es egal, welche $x$-Werte-Folge $(x_n)$ mit $x_n \rightarrow +\infty$ (bzw. für $x \rightarrow -\infty$) man vorgibt. |
|
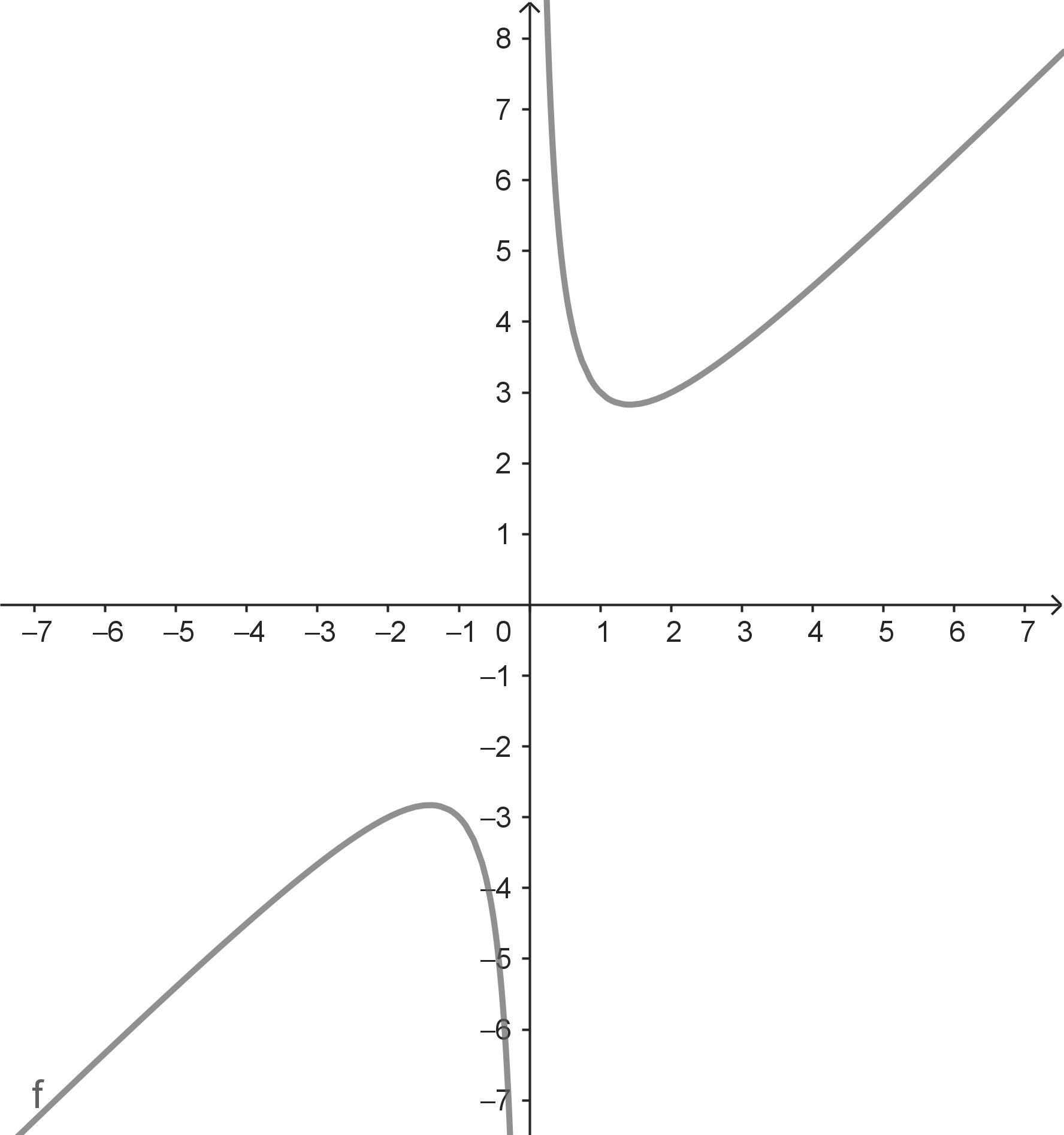
Für $x \rightarrow +\infty$ gilt $f(x) \rightarrow +\infty$.
Das siehtman, wenn man eine $x$-Werte-Folge $(x_n)$ mit $x_n \rightarrow +\infty$ durchläuft und dabei die Folge $(f(x_n))$ der zugehörigen Funktionswerte betrachtet. Entsprechend siehtman: Für $x \rightarrow -\infty$ gilt $f(x) \rightarrow -\infty$. Die Funktion hat hier für $x \rightarrow +\infty$ bzw. für $x \rightarrow -\infty$ keine endlichen Grenzwerte. Man kann aber dennoch Aussagen über das Grenzverhalten treffen. |
|
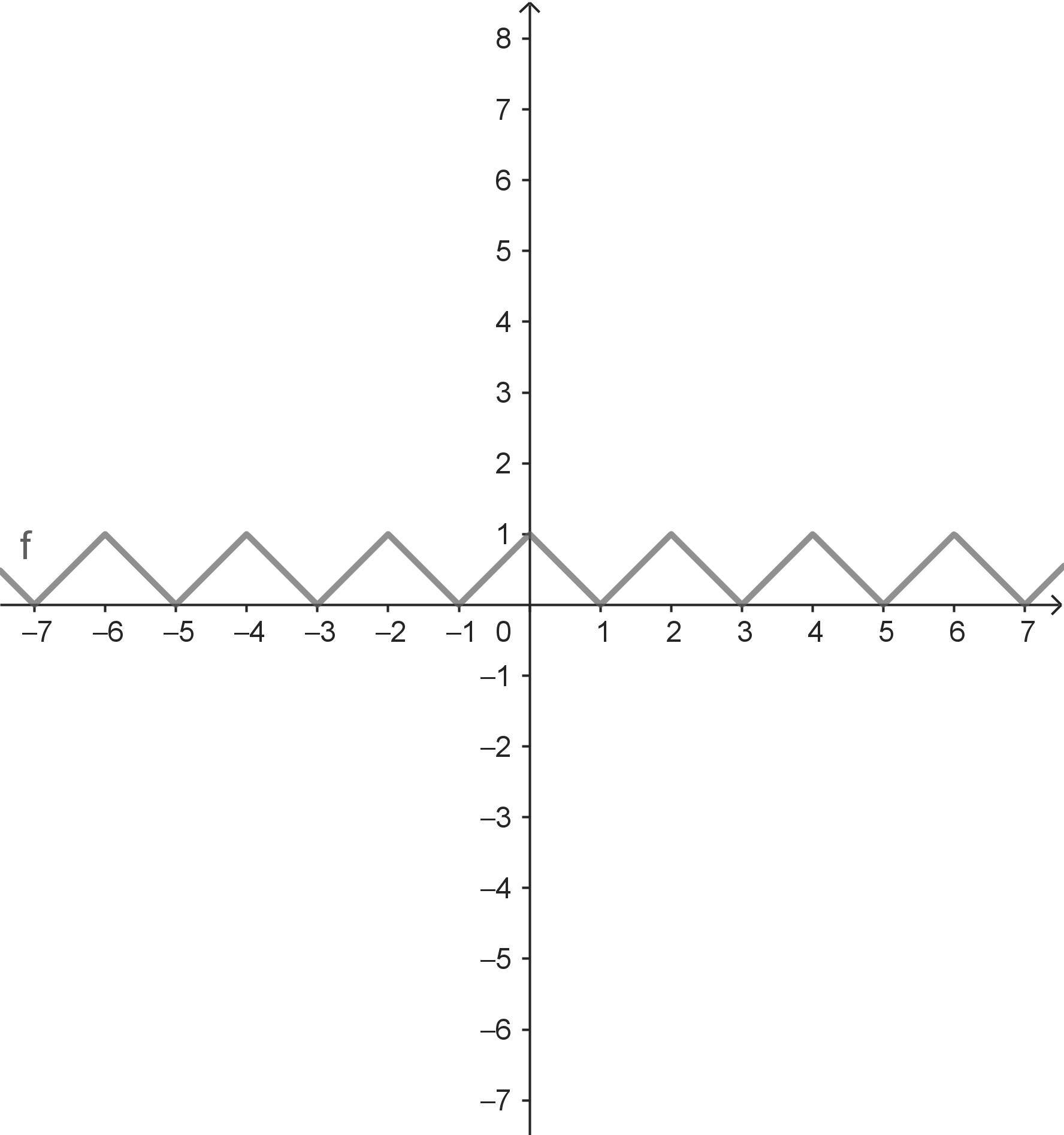
Bei der Zickzack-Funktionstabilisieren sich für $x \rightarrow +\infty$ (bzw. für $x \rightarrow -\infty$) die Funktionswerte nicht. Es gibt hier durchaus $x$-Werte-Folgen, für die sich die zugehörigen Funktionswerte bei einer Zahl stabilisieren. Allerdings liefern hier unterschiedliche $x$-Werte-Folgen ein unterschiedliches Grenzverhalten. Bei dieser Funktion gibt es demnach keinen Grenzwert für $x \rightarrow +\infty$ (bzw. für $x \rightarrow -\infty$). |
Wir nutzen diese Erkenntnisse, um den Grenzwertbegriff bei Funktionen präzise festzulegen.
Grenzwert einer Funktion für $x \rightarrow \pm\infty$
Eine Funktion $f$ hat für $x \rightarrow +\infty$ (bzw. $x \rightarrow -\infty$) den Grenzwert $g$ genau dann, wenn folgende Bedingung erfüllt ist:
Für jede Folge von $x$-Werten $(x_n)$ mit $x_n \rightarrow +\infty$ (bzw. $x_n \rightarrow -\infty$) – mit $x$-Werten aus der Definitionsmenge von $f$ – konvergiert die zugehörige Folge von Funktionswerten $(f(x_n))$ gegen den Grenzwert $g$.
Schreibweise: $\lim \limits_{x \to +\infty} f(x) = g$ bzw. $\lim \limits_{x \to -\infty} f(x) = g$
Aufgabe 1
Erläutere: Die vorliegende Definition des Grenzwertbegriffs für Funktionen verwendet die Grenzwertdefinition für Folgen.
