Zusammenfassung - Grenzwerte bei Funktionen

Grenzverhalten von Funktionen

Funktionen werden in vielen Anwendungsbereichen benutzt, um Abhängigkeiten zwischen Größen zu erfassen. Man beschreibt dabei, wie sich eine Größe in Abhängigkeit von einer anderen verändert.

In der Physik beschreibt man beispielsweise mit einer Gravitationsfunktion, wie sich die Anziehungskraft zwischen zwei Körpern mit vorgegebenen Massen verändert, wenn man den Abstand der Körper verändert. Im Applet wird die Gravitationskraft zwischen der Erde und einem Körper der Masse 1kg mit einer solche Gravitationsfunktion dargestellt. Beachte, dass die beiden Objekte – die Erde und der Körper – hier punktförmig dargestellt werden.

In solchen Anwendungssituation interessieren oft folgende Fragestellungen:

• Wie verhalten sich die Funktionswerte (d.h.: die Werte der zugeordneten Größe), wenn die $x$-Werte (d.h.: die Ausgangswerte) betragsmäßig immer größer werden, wenn also $x$ gegen $+\infty$ oder gegen $-\infty$ geht?
• Wie verhalten sich die Funktionswerte (d.h.: die Werte der zugeordneten Größe), wenn die $x$-Werte (d.h.: die Ausgangswerte) sich einer besonderen Stelle $a$ nähern – an der die Funktion nicht definiert ist?

Zur Klärung solcher Fragen nutzt man Grenzwerte bei Funktionen.

Grenzwert einer Funktion für $x \rightarrow \pm\infty$

Betrachte das Grenzverhalten bei den folgenden Beispielfunktionen.

Situation	Grenzverhalten
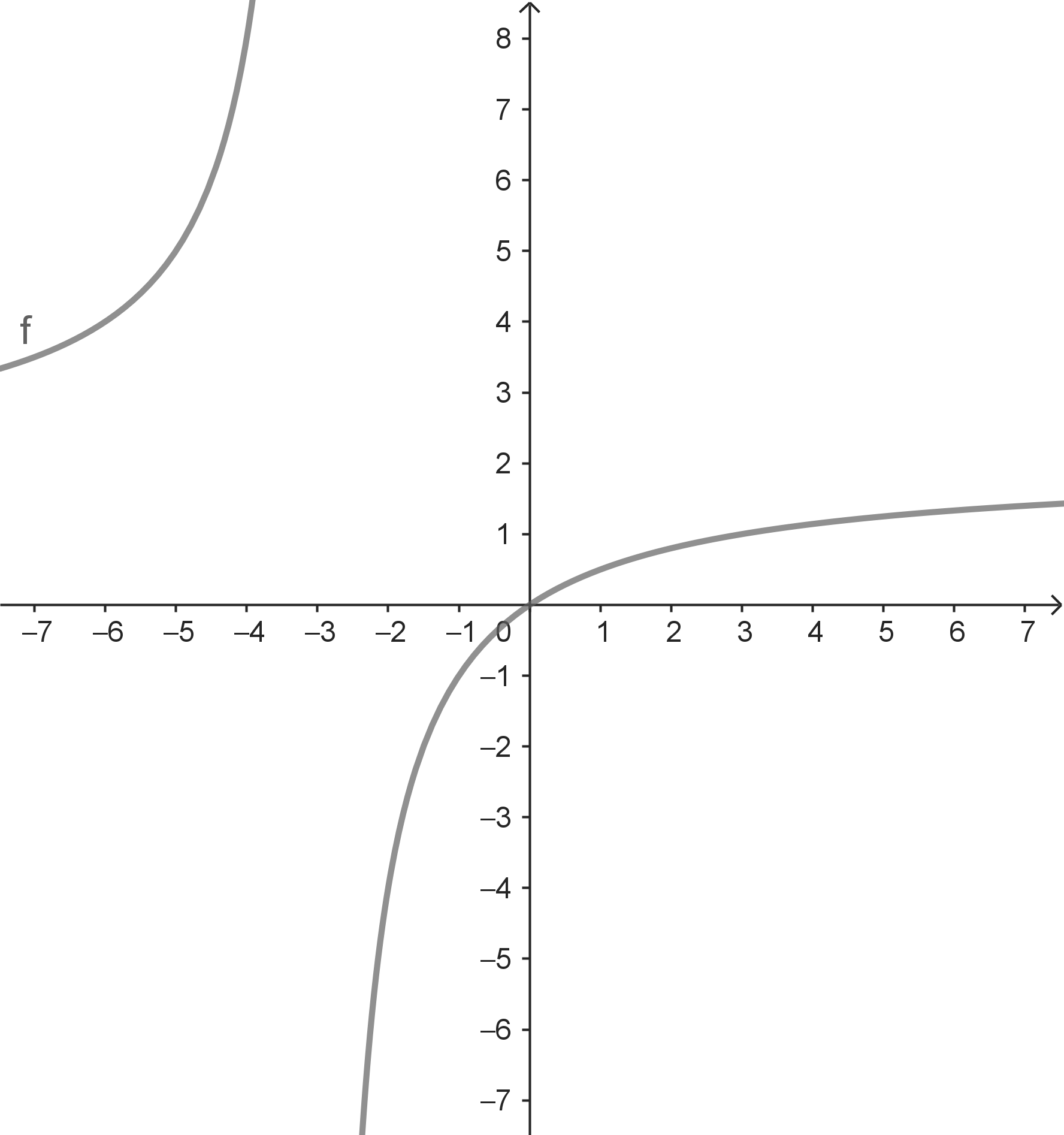
	Die Funktionswerte $f(x)$ stabilisieren sich für $x \rightarrow +\infty$ (bzw. für $x \rightarrow -\infty$) bei der Zahl $g = 2$. Das sieht man, wenn man eine $x$-Werte-Folge $(x_n)$ mit $x_n \rightarrow +\infty$ (bzw. für $x \rightarrow -\infty$) durchläuft und dabei die Folge $(f(x_n))$ der zugehörigen Funktionswerte betrachtet. Dabei ist es egal, welche $x$-Werte-Folge $(x_n)$ mit $x_n \rightarrow +\infty$ (bzw. für $x \rightarrow -\infty$) man vorgibt.
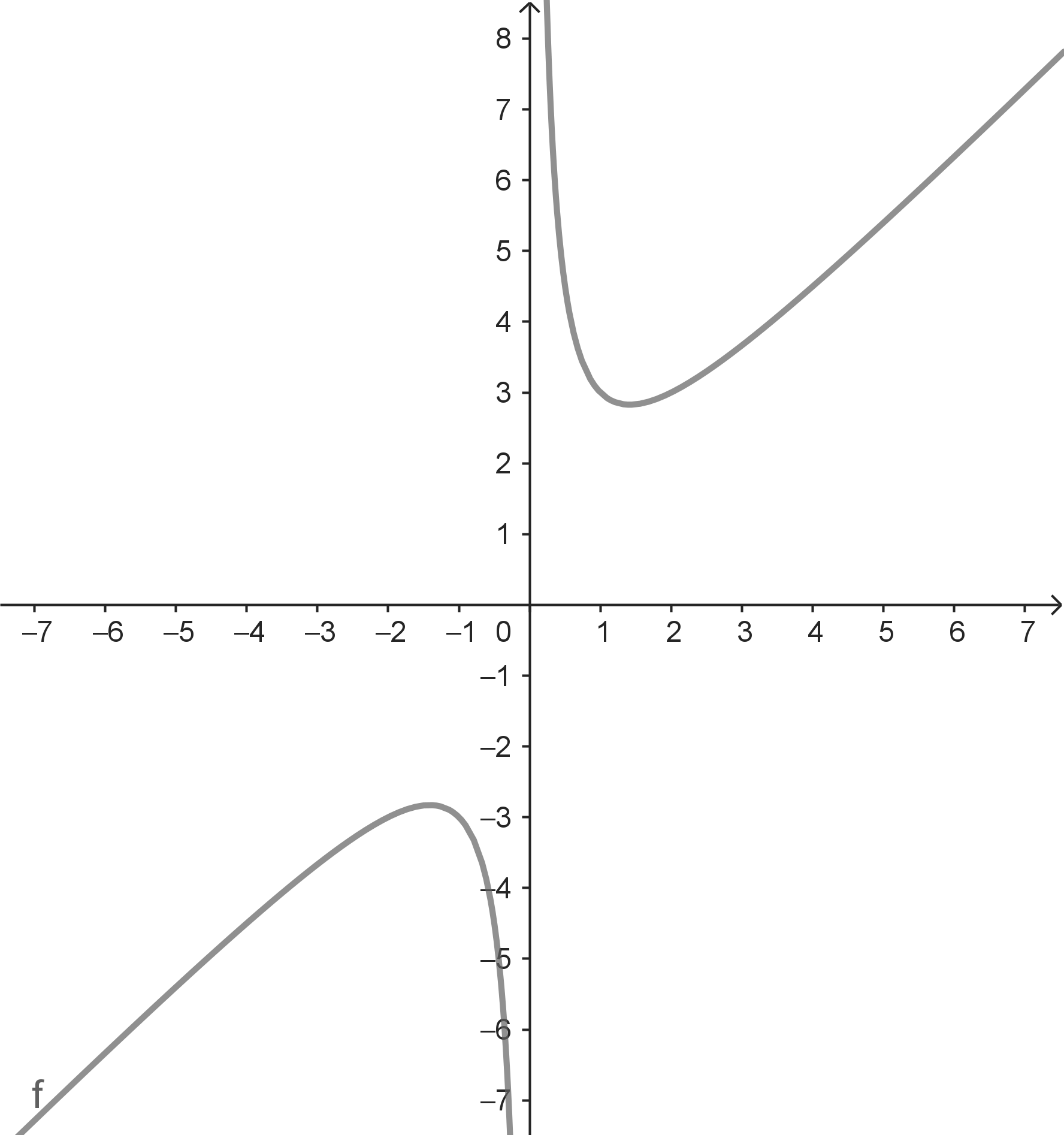
	Für $x \rightarrow +\infty$ gilt $f(x) \rightarrow +\infty$. Das sieht man, wenn man eine $x$-Werte-Folge $(x_n)$ mit $x_n \rightarrow +\infty$ durchläuft und dabei die Folge $(f(x_n))$ der zugehörigen Funktionswerte betrachtet. Entsprechend sieht man: Für $x \rightarrow -\infty$ gilt $f(x) \rightarrow -\infty$. Die Funktion hat hier für $x \rightarrow +\infty$ bzw. für $x \rightarrow -\infty$ keine endlichen Grenzwerte. Man kann aber dennoch Aussagen über das Grenzverhalten treffen.
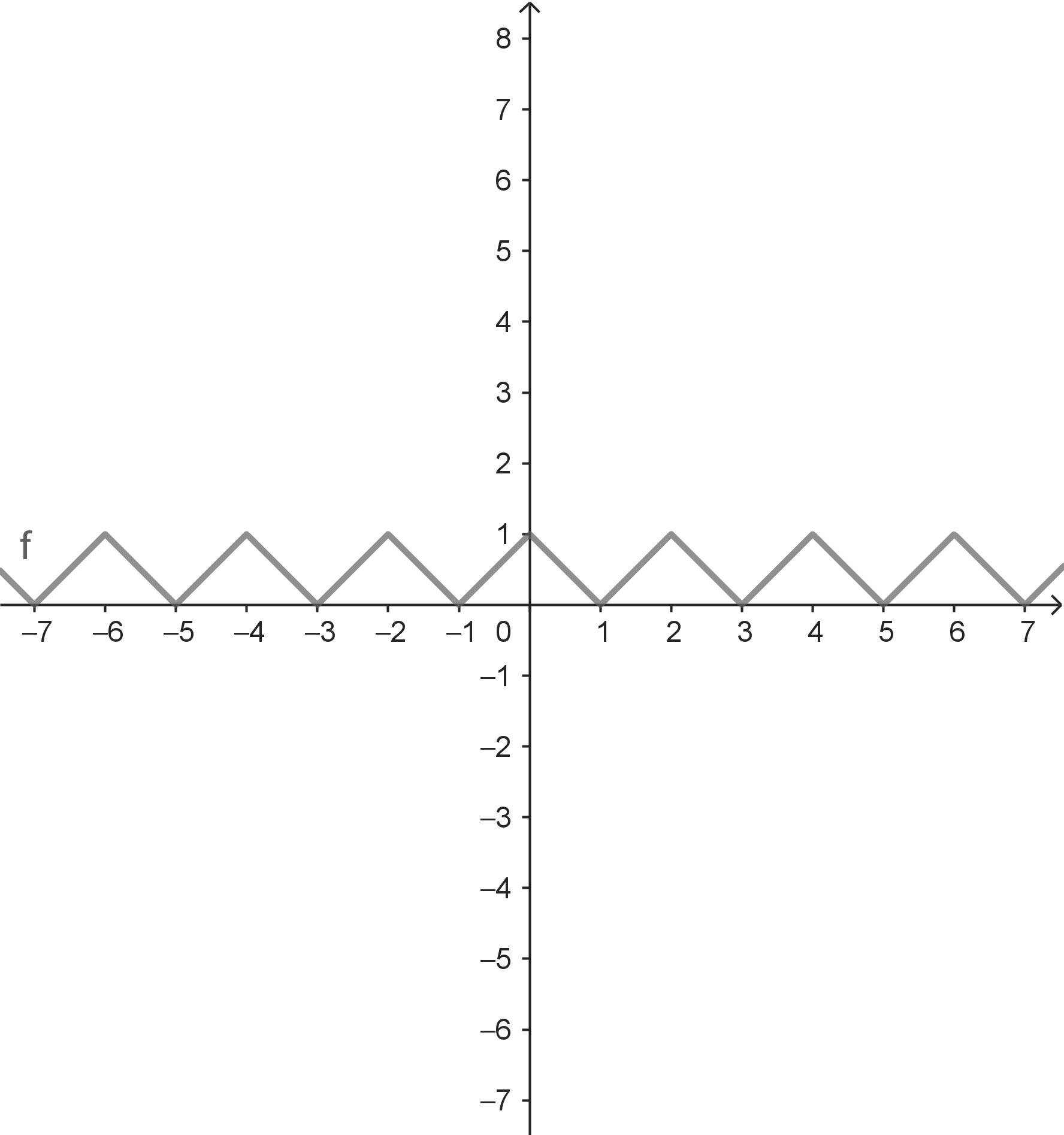
	Bei der Zickzack-Funktion stabilisieren sich für $x \rightarrow +\infty$ (bzw. für $x \rightarrow -\infty$) die Funktionswerte nicht. Es gibt hier durchaus $x$-Werte-Folgen, für die sich die zugehörigen Funktionswerte bei einer Zahl stabilisieren. Allerdings liefern hier unterschiedliche $x$-Werte-Folgen ein unterschiedliches Grenzverhalten. Bei dieser Funktion gibt es demnach keinen Grenzwert für $x \rightarrow +\infty$ (bzw. für $x \rightarrow -\infty$).

Wir nutzen diese Erkenntnisse, um den Grenzwertbegriff bei Funktionen präzise festzulegen.

Beachte: Die vorliegende Definition des Grenzwertbegriffs für Funktionen verwendet die Grenzwertdefinition für Folgen.

Grenzwert einer Funktion für $x \rightarrow a$

Betrachte das Grenzverhalten bei den folgenden Beispielfunktionen.

Funktion	Grenzverhalten an einer Stelle
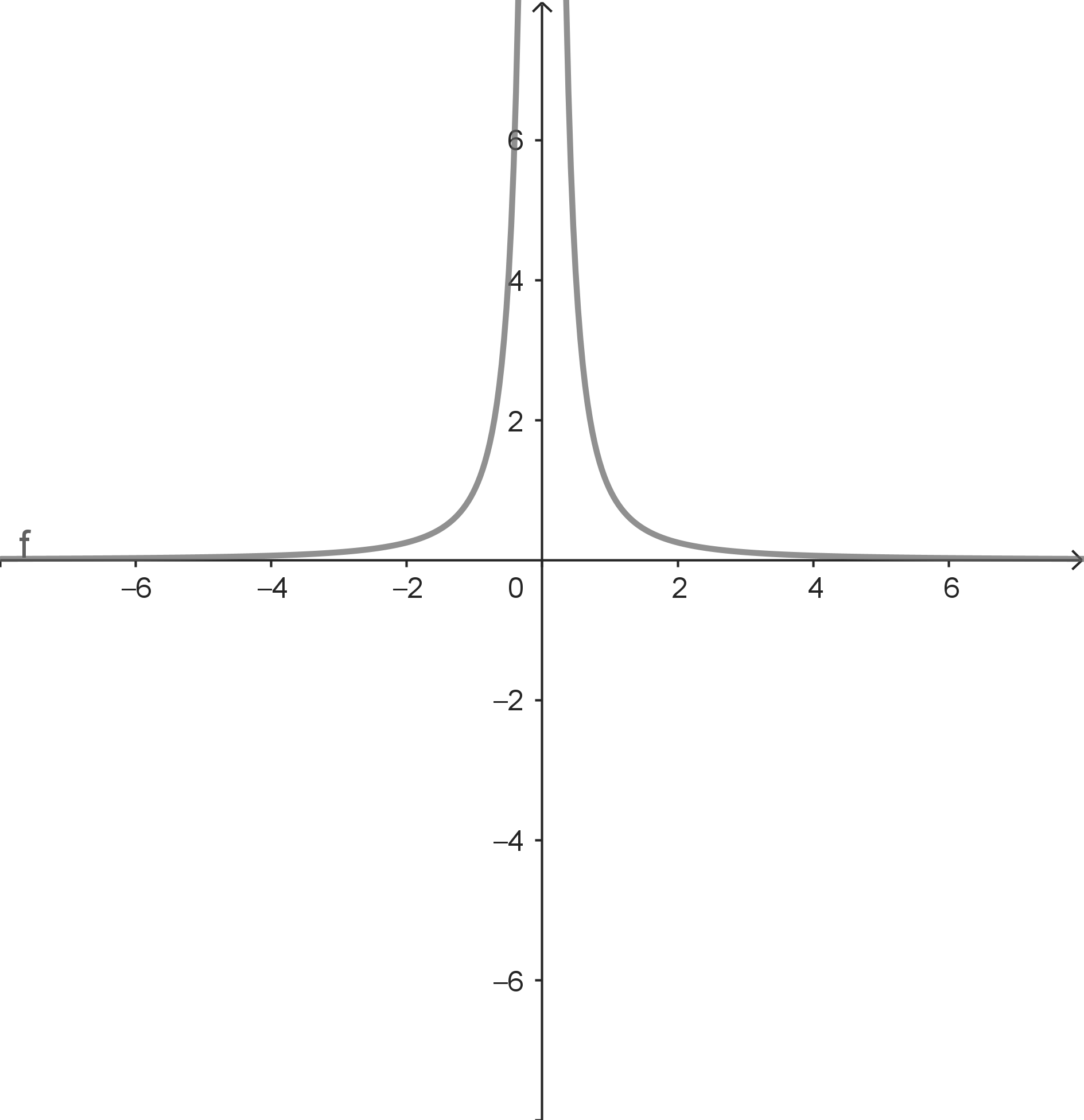
$f(x) = \dfrac{1}{x^2}$	Stelle: $a = 0$ Beachte: $f$ ist an der Stelle $a = 0$ nicht definiert. Für $x \rightarrow a$ mit $x > a$ gilt $f(x) \rightarrow +\infty$. Für $x \rightarrow a$ mit $x \text{ < } a$ gilt $f(x) \rightarrow +\infty$. Es existiert kein endlicher Grenzwert.
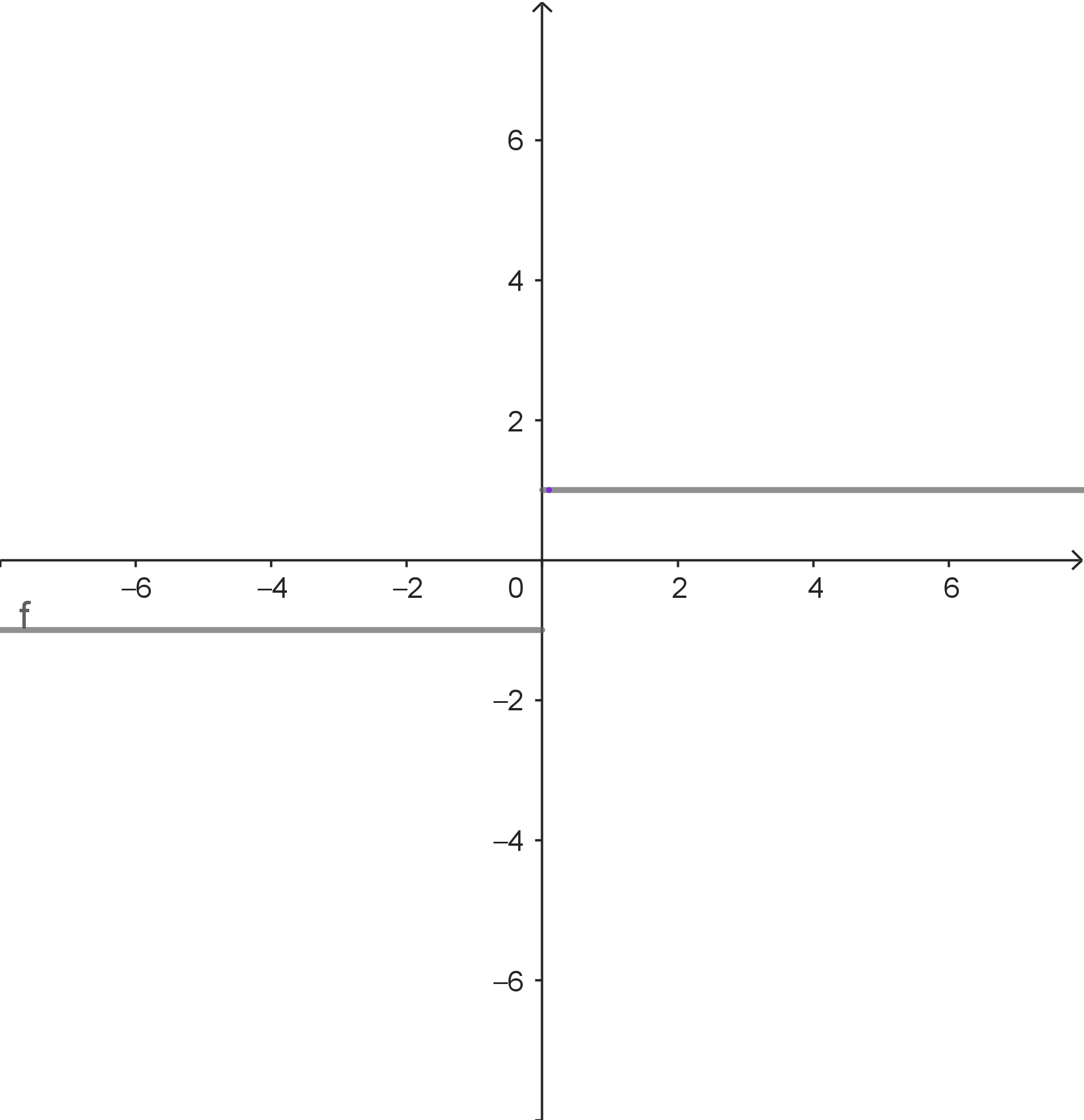
$f(x) = \dfrac{x}{|x|}$	Stelle: $a = 0$ Beachte: $f$ ist an der Stelle $a = 0$ nicht definiert. Für $x \rightarrow a$ mit $x > a$ gilt $f(x) \rightarrow 1$. Für $x \rightarrow a$ mit $x \text{ < } a$ gilt $f(x) \rightarrow -1$. Für unterschiedliche Annäherungsfolgen ergeben sich unterschiedliche Grenzwerte. Es existiert also kein eindeutiger Grenzwert.
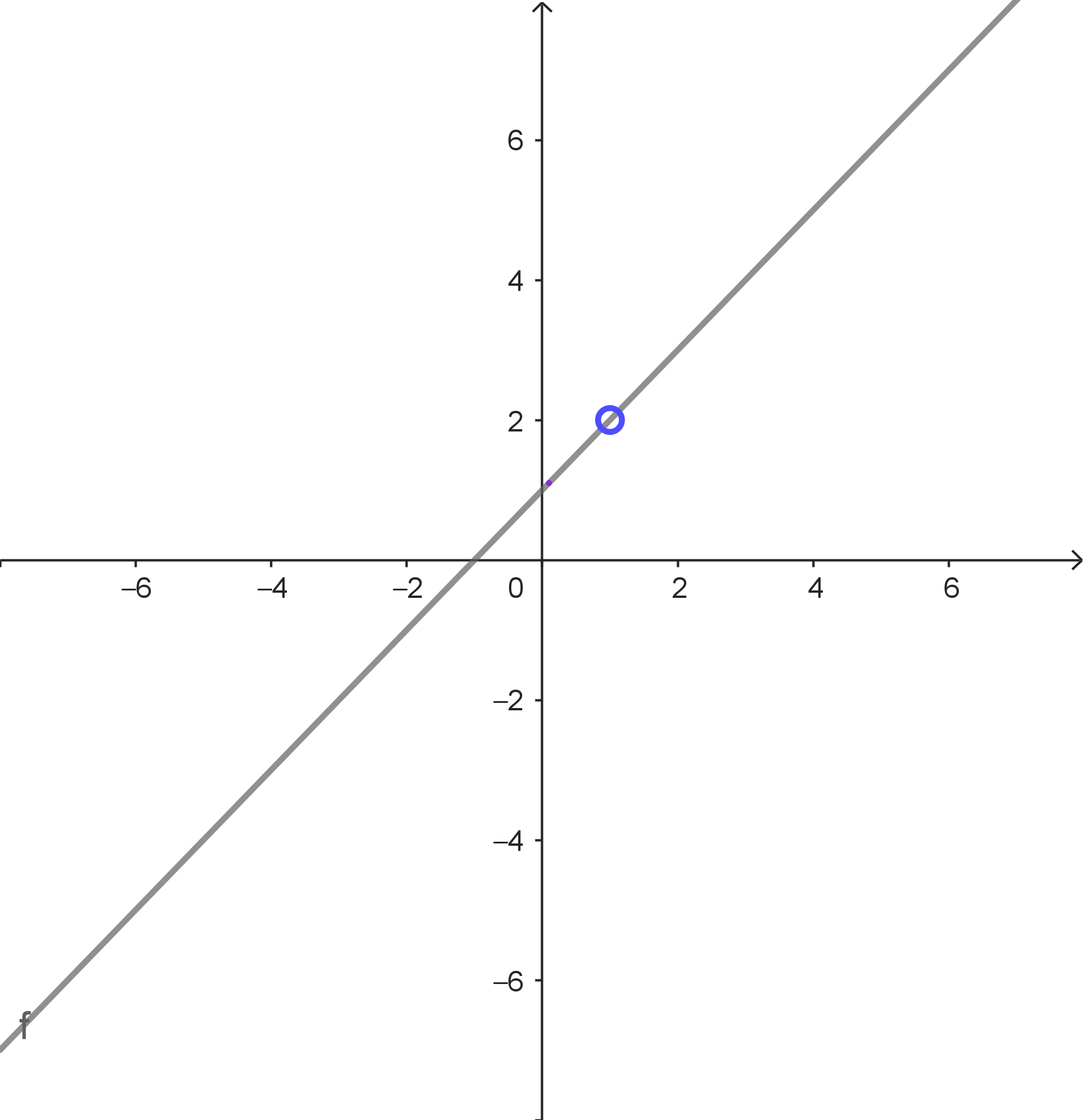
$f(x) = \dfrac{x^2-1}{x-1}$	Stelle: $a = 1$ Beachte: $f$ ist an der Stelle $a = 1$ nicht definiert. Für $x \rightarrow a$ gilt $f(x) \rightarrow 2$. Für jede Annäherungsfolge erhält man den Grenzwert $g = 2$.
$f(x) = \sin(\frac{1}{x})$	Stelle: $a = 0$ Beachte: $f$ ist an der Stelle $a = 0$ nicht definiert. Unterschiedliche Annäherungsfolgen haben ein unterschiedliches Grenzverhalten. Es existiert kein Grenzwert.
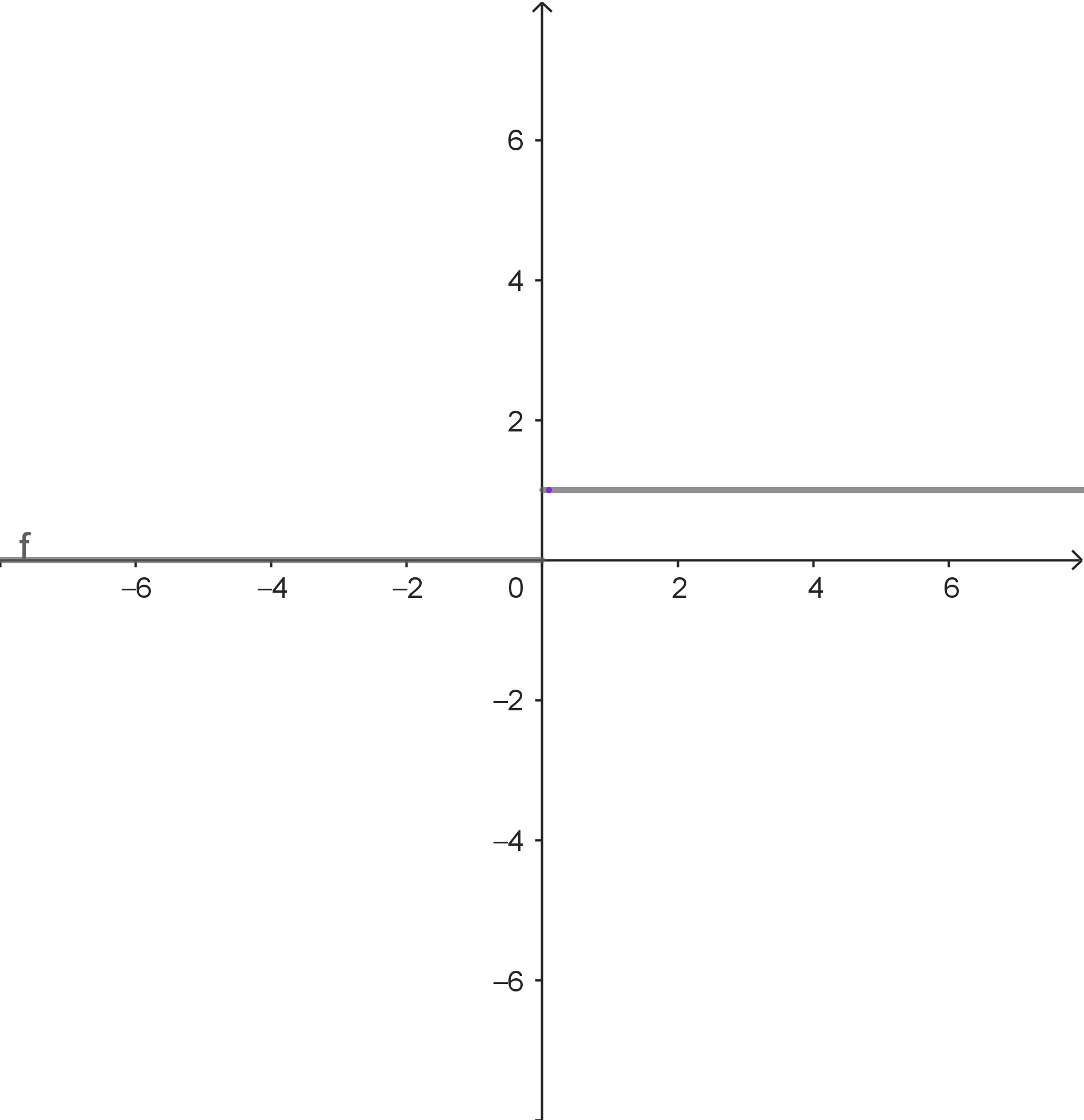
$f(x) = \begin{cases} 1 & \text{wenn } x > 0 \\ 0 & \text{wenn } x \leq 0 \end{cases}$	Stelle: $a = 0$ Beachte: $f$ ist an der Stelle $a = 0$ definiert. Für $x \rightarrow a$ mit $x > a$ gilt $f(x) \rightarrow 1$. Für $x \rightarrow a$ mit $x \text{ < } a$ gilt $f(x) \rightarrow 0$. Für unterschiedliche Annäherungsfolgen ergeben sich unterschiedliche Grenzwerte. Es existiert also kein eindeutiger Grenzwert.

Grenzbetrachtungen an einer Stelle führt man aus, wenn die Funktion an der Stelle nicht definiert ist. Das letzte Beispiel zeigt, dass solche Grenzwertbetrachtungen aber auch sinnvoll sind, wenn die Funktion an der Stelle definiert ist.

Der entscheidende Punkt für die Existenz eines (endlichen) Grenzwerts einer Funktion an einer Stelle ist, dass sich die Funktionswerte immer bei derselben Grenzwertzahl stabilisieren, egal wie man sich der betrachteten Stelle annähert.

Wir nutzen diese Vorstellung, um den Grenzwertbegriff bei Funktionen präzise festzulegen.

Beachte: Die vorliegende Definition des Grenzwertbegriffs für Funktionen verwendet ebenfalls die Grenzwertdefinition für Folgen.