Vertiefung
Zur Orientierung
Im letzten Abschnitt hast du bereits das Grenzverhalten von Funktionen für $x \rightarrow a$ bestimmt. Wir sind dort von einem intuitiven Grenzwertverständnis ausgegangen. In diesem Abschnitt holen wir eine präzise Festlegung des Grenzwertbegriff bei Funktionen nach.
Eine Definition entwickeln
Im letzten Abschnitt hast du folgende Grenzverhaltenssituationen betrachtet.
| Funktion | Grenzverhalten an einer Stelle |
|---|---|
$f(x) = \dfrac{1}{x^2}$
Graph einblenden
|
Stelle: $a = 0$ Beachte: $f$ ist an der Stelle $a = 0$ nicht definiert. Für $x \rightarrow a$ mit $x > a$ gilt $f(x) \rightarrow +\infty$. Für $x \rightarrow a$ mit $x \text{ < } a$ gilt $f(x) \rightarrow +\infty$. Es existiert kein endlicher Grenzwert. |
$f(x) = \dfrac{x}{|x|}$
Graph einblenden
|
Stelle: $a = 0$ Beachte: $f$ ist an der Stelle $a = 0$ nicht definiert. Für $x \rightarrow a$ mit $x > a$ gilt $f(x) \rightarrow 1$. Für $x \rightarrow a$ mit $x \text{ < } a$ gilt $f(x) \rightarrow -1$. Für unterschiedliche Annäherungsfolgen ergeben sich unterschiedliche Grenzwerte. Es existiert also kein eindeutiger Grenzwert. |
$f(x) = \dfrac{x^2-1}{x-1}$
Graph einblenden
|
Stelle: $a = 1$ Beachte: $f$ ist an der Stelle $a = 1$ nicht definiert. Für $x \rightarrow a$ gilt $f(x) \rightarrow 2$. Für jede Annäherungsfolge erhält man den Grenzwert $g = 2$. |
$f(x) = \sin(\frac{1}{x})$
Graph einblenden
|
Stelle: $a = 0$ Beachte: $f$ ist an der Stelle $a = 0$ nicht definiert. Unterschiedliche Annäherungsfolgen haben ein unterschiedliches Grenzverhalten. |
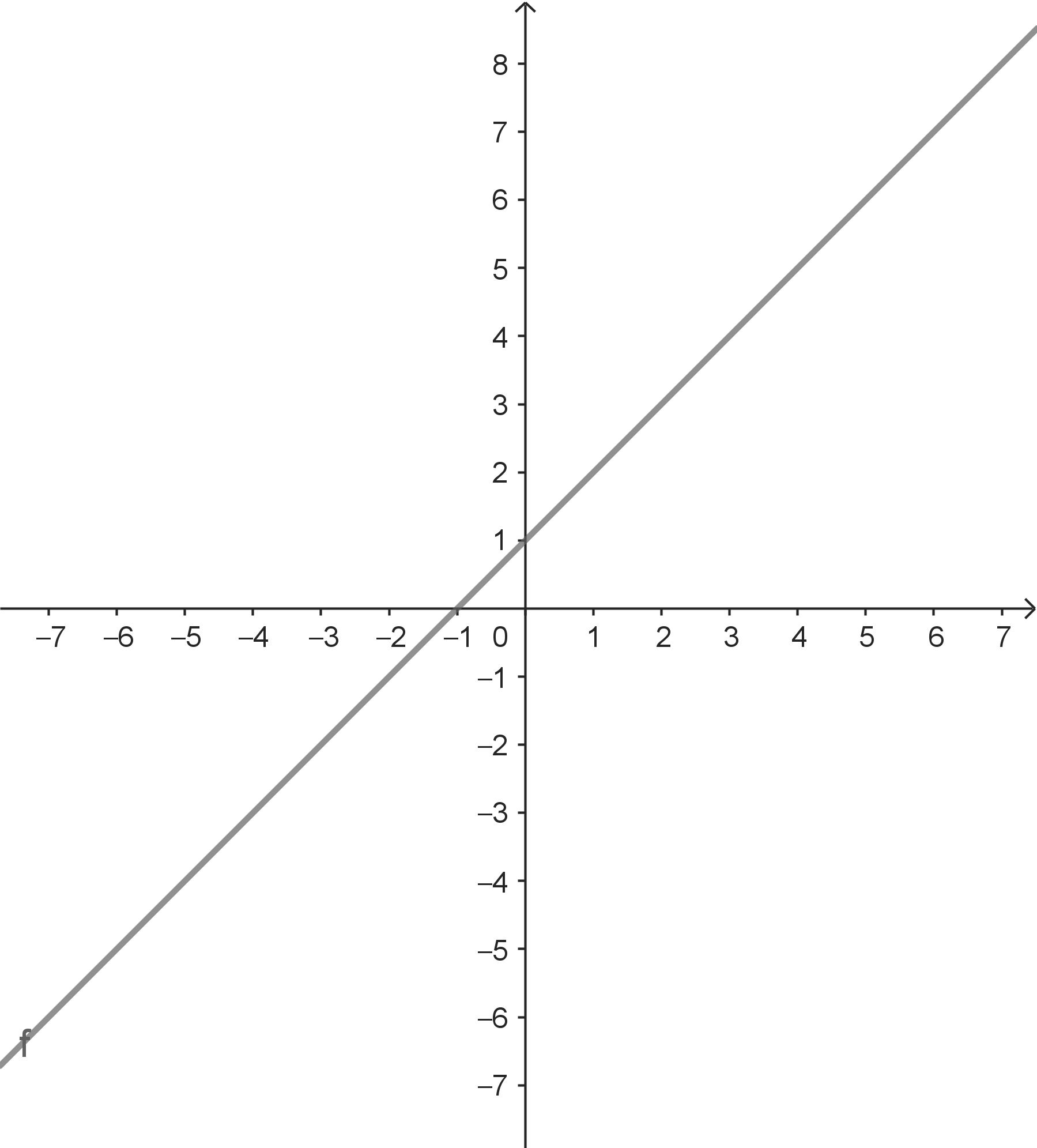
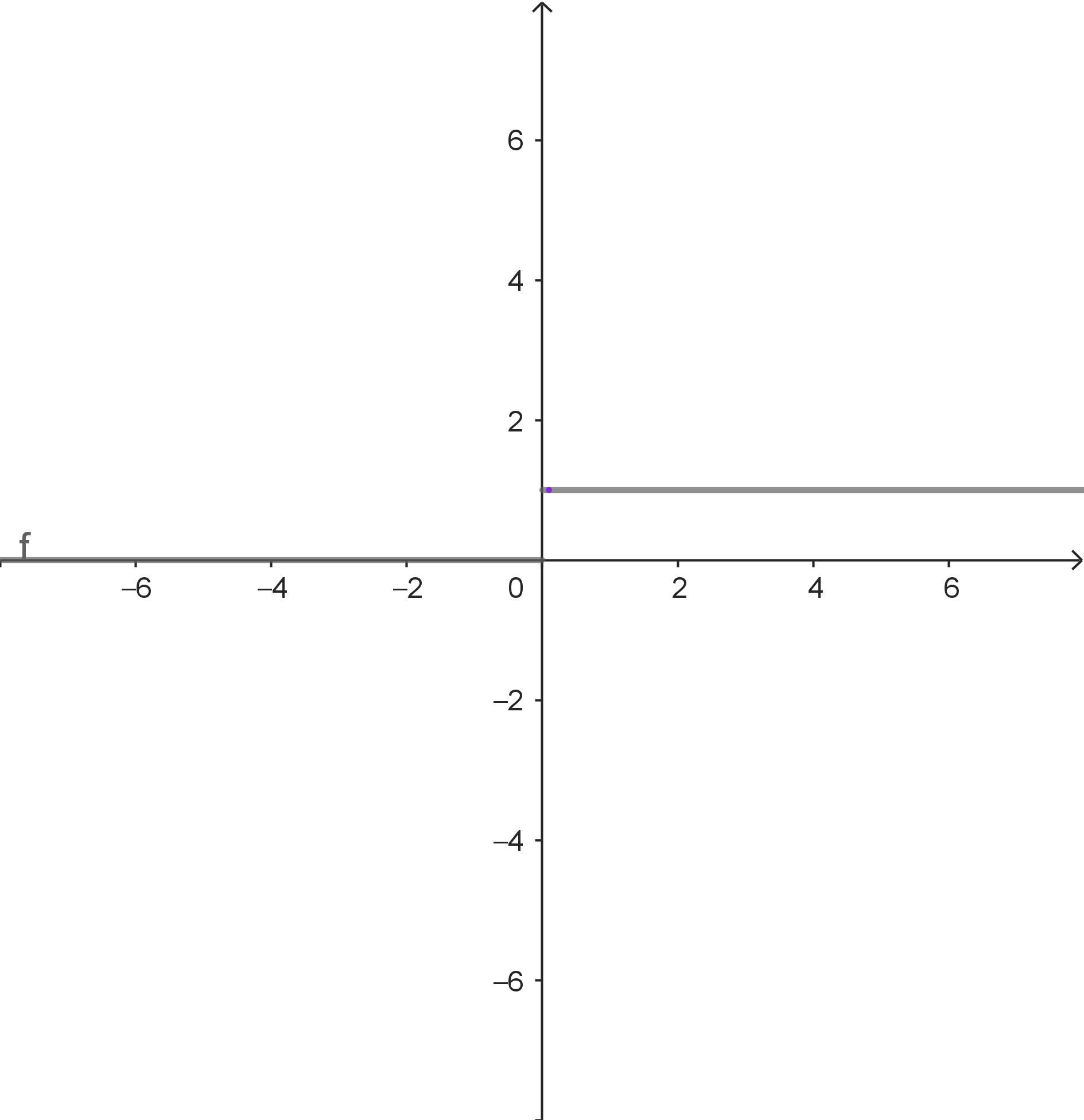
$f(x) = \begin{cases} 1 & \text{wenn } x > 0 \\ 0 & \text{wenn } x \leq 0 \end{cases}$
Graph einblenden
|
Stelle: $a = 0$ Beachte: $f$ ist an der Stelle $a = 0$ definiert. Für $x \rightarrow a$ mit $x > a$ gilt $f(x) \rightarrow 1$. Für $x \rightarrow a$ mit $x \text{ < } a$ gilt $f(x) \rightarrow 0$. Für unterschiedliche Annäherungsfolgen ergeben sich unterschiedliche Grenzwerte. Es existiert also kein eindeutiger Grenzwert. |
Grenzbetrachtungen an einer Stelle führt man aus, wenn die Funktion an der Stelle nicht definiert ist. Das letzte Beispiel zeigt, dass solche Grenzwertbetrachtungen aber auch sinnvoll sind, wenn die Funktion an der Stelle definiert ist.
Der entscheidende Punkt für die Existenz eines (endlichen) Grenzwerts einer Funktion an einer Stelle ist, dass sich die Funktionswerte immer bei derselben Grenzwertzahl stabilisieren, egal wie man sich der betrachteten Stelle annähert.
Wir nutzen diese Vorstellung, um den Grenzwertbegriff bei Funktionen präzise festzulegen.
Grenzwert einer Funktion für $x \rightarrow a$
Eine Funktion $f$ hat für $x \rightarrow a$ den Grenzwert $g$ genau dann, wenn folgende Bedingung erfüllt ist:
Für jede Folge $(x_n)$ von $x$-Werten (aus der Definitionsmenge von $f$, die ungleich $a$ sind) mit $x_n \rightarrow a$ konvergiert die zugehörige Folge $(f(x_n))$ von Funktionswerten gegen den Grenzwert $g$.
Schreibweise: $\lim \limits_{x \to a} f(x) = g$
Aufgabe 1
Erläutere: Die vorliegende Definition des Grenzwertbegriffs für Funktionen verwendet die Grenzwertdefinition für Folgen.
